Authors : Jason Wei, Xuezhi Wang, Dale Schuurmans, Maarten Bosma, Brian Ichter, Fei Xia, Ed Chi, Quoc Le, Denny Zhou
Institution : Google Research, Brain Team
Publication Date : Jan 10, 2023
paper : https://arxiv.org/abs/2201.11903
abstract
일련의 중간 추론 단계인 사고의 연쇄를 생성하는 것이 어떻게 대규모 언어 모델의 복잡한 추론 수행 능력을 크게 향상시키는지 살펴봅니다. 특히, 몇 가지 연쇄적 사고의 예시를 프롬프트의 예시로 제공하는 연쇄적 사고 프롬프트라는 간단한 방법을 통해 LLM에서 이러한 추론 능력이 어떻게 자연스럽게 나타나는지 보여줍니다. 세 가지 대규모 언어 모델에 대한 실험에 따르면 사고 연쇄 프롬프트는 다양한 산술, 상식 및 상징적 추론 작업에서 수행 능력을 향상시키는 것으로 나타났습니다. 예를 들어, 540B 매개변수 언어 모델에 8개의 연쇄 사고 예시만으로 프롬프트하면 수학 단어 문제의 GSM8K 벤치마크에서 최첨단 정확도를 달성하여 검증기를 통해 세밀하게 조정된 GPT-3을 능가하였습니다.
정리
이 논문에서는 대형 언어 모델의 복잡한 추론 작업 수행 능력을 향상시키는 방법인 사고의 연쇄(chain of thought)에 대해 탐구합니다. 사고의 연쇄란 문제를 해결하는 과정에서 연속적인 추론 단계를 생성하여 최종 답변에 도달하는 방식입니다. 충분한 크기의 언어 모델에서는 몇 가지 사고의 연쇄 예시를 제공함으로써 사고의 연쇄 추론 능력이 자연스럽게 나타납니다. 이를 통해 산술, 상식, 기호적 추론 작업 등 다양한 작업에서 성능이 향상됨을 실험적으로 입증하였습니다.
사고의 연쇄는 복잡한 추론 작업을 해결하기 위해 문제를 중간 단계로 분해하고 각 단계를 해결하여 최종 답을 도출하는 과정입니다.
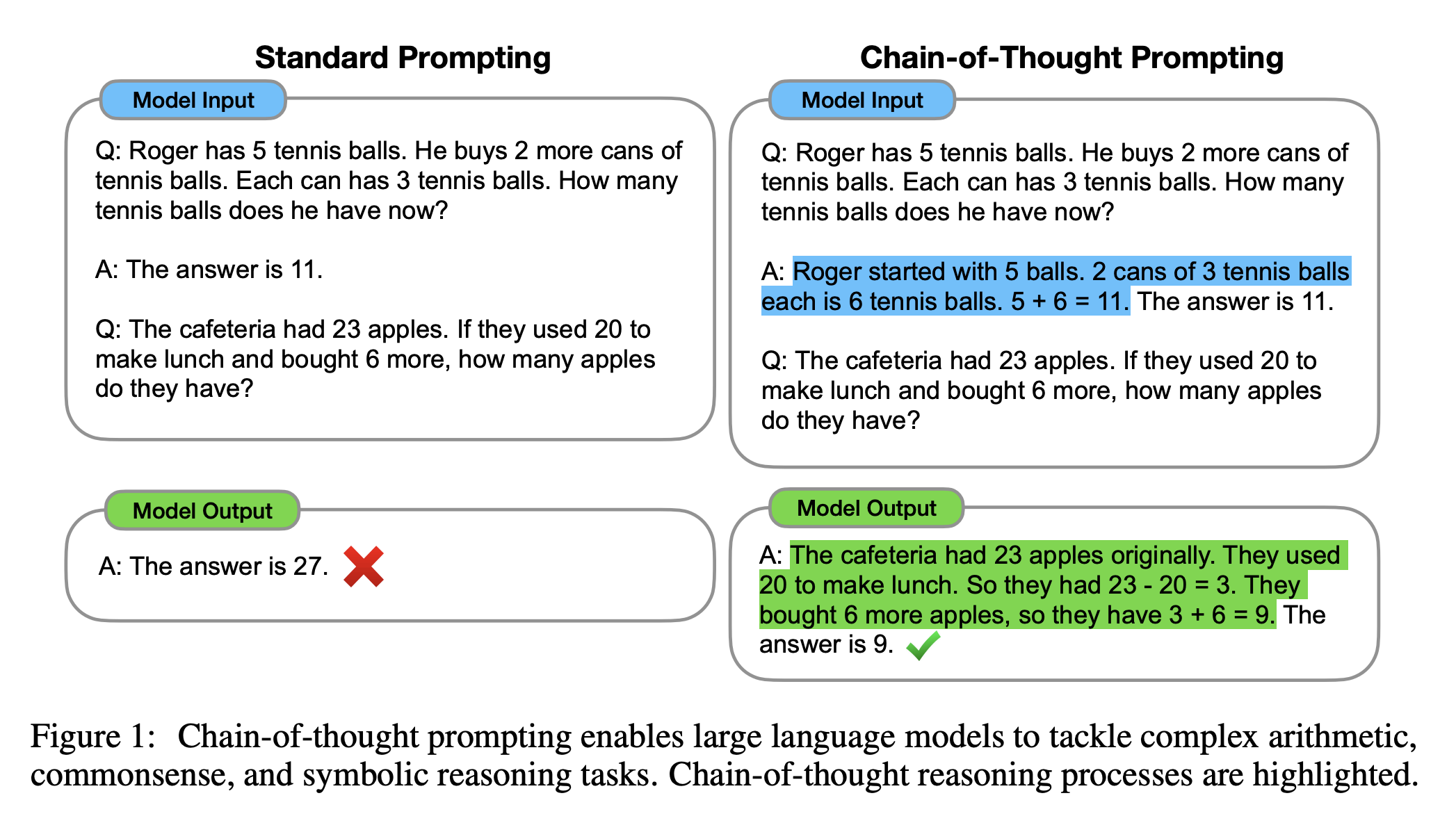
예를 들어, “로저에게 5개의 공이 있다. 3개씩 들어있는 2개의 테니스 볼 캔은 총 6개다. 5+6=11. 답은 11 이다.”와 같은 방식으로 문제를 해결합니다. 이러한 사고의 연쇄를 사용하는 언어 모델에는 다음과 같은 장점이 있습니다.
사고의 연쇄를 사용하면 여러 단계의 문제를 중간 단계로 분해할 수 있어, 더 많은 추론 단계가 필요한 문제에 추가 계산을 할당할 수 있습니다. 사고의 연쇄는 모델의 동작에 대한 해석 가능한 창을 제공하며, 특정 답변에 도달하는 방법을 제안하고 추론 경로가 잘못된 경우 디버깅할 기회를 제공합니다. 사고의 연쇄 추론은 수학 문제, 상식 추론, 기호 조작 등의 작업에 사용할 수 있으며, 원칙적으로 사람이 언어를 통해 해결할 수 있는 모든 작업에 적용할 수 있습니다. 충분히 큰 규모의 언어 모델에서는 사고의 연쇄 시퀀스를 몇 가지 예시에 포함시키는 것만으로 사고의 연쇄 추론을 쉽게 유도할 수 있습니다. 실험 결과, 사고의 연쇄를 사용하는 것은 모델 규모에 따른 새로운 능력이 나타나는 것으로 확인되었습니다. 작은 모델에서는 사고의 연쇄가 성능에 긍정적인 영향을 미치지 않지만, 약 100B 파라미터 정도의 큰 모델에서는 성능 향상이 이루어집니다. 작은 규모의 모델에서는 유창하지만 논리적이지 않은 사고의 연쇄가 생성되어, 표준 프롬프팅보다 성능이 낮아집니다.
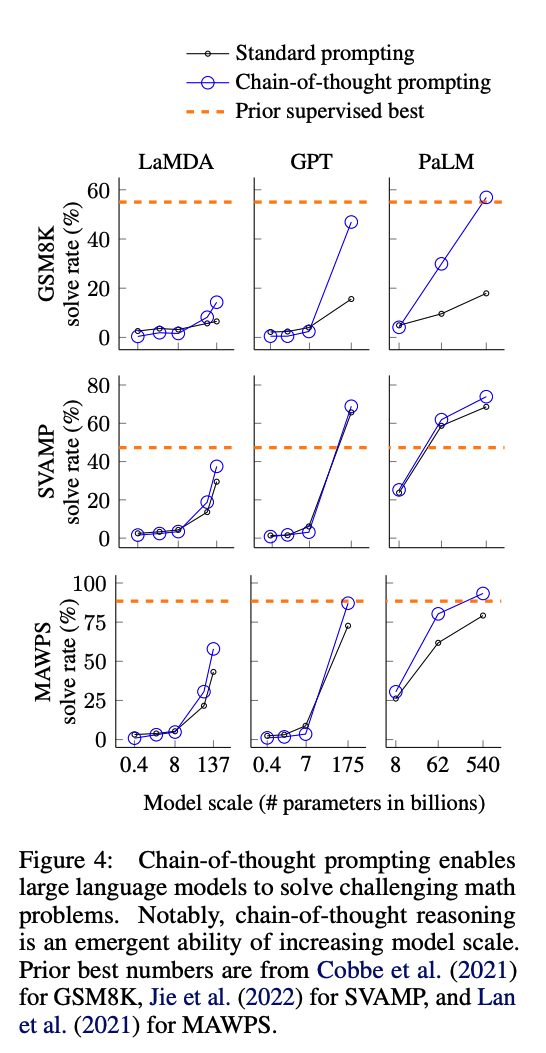
또한, 사고의 연쇄 프롬프팅은 더 복잡한 문제에 대한 성능 향상이 더 큽니다. 예를 들어, 기준 성능이 가장 낮은 GSM8K 데이터셋에서는 가장 큰 GPT와 PaLM 모델의 성능이 두 배 이상 향상되었습니다. 반면, SingleOp와 같이 한 단계만으로 해결할 수 있는 가장 쉬운 부분 집합의 경우 성능 개선이 부정적이거나 매우 작았습니다.
마지막으로, GPT-3 175B와 PaLM 540B를 사용한 사고의 연쇄 프롬프팅은 이전 최고 성능과 유사하게 나타났으며, 이는 일반적으로 레이블이 지정된 학습 데이터셋에서 작업별 모델을 미세 조정하는 방식입니다. 이를 통해 PaLM 540B는 사고의 연쇄 프롬프팅을 사용하여 GSM8K, SVAMP, MAWPS에서 새로운 최고 성능을 달성했습니다. 다른 두 데이터셋인 AQuA와 ASDiv에서도, 사고의 연쇄 프롬프팅을 사용한 PaLM은 최고 성능과 2% 이내의 차이를 보였습니다.
사고의 연쇄 프롬프팅이 작동하는 이유를 더 잘 이해하기 위해, GSM8K에서 LaMDA 137B로 생성된 사고의 연쇄를 수동으로 검토했습니다. 50개의 무작위 예제 중 모델이 올바른 최종 답변을 반환한 경우, 생성된 사고의 연쇄가 모두 논리적이고 수학적으로 올바른 것으로 확인되었습니다. 그러나 우연히 정답에 도달한 두 가지 경우를 제외하고는 말입니다. 또한, 모델이 잘못된 답변을 제공한 50개의 무작위 샘플을 검토했습니다. 분석한 결과, 사고의 연쇄의 46%는 거의 정확하였으나, 작은 실수들(계산 오류, 기호 매핑 오류 또는 누락된 추론 단계)이 있었습니다. 나머지 54% 는 의미론적 이해나 일관성에서 주요 오류가 있었습니다.
스케일이 사고의 연쇄 추론 능력을 향상시키는 이유를 조금 더 이해하기 위해, PaLM 62B가 저지른 오류와 그 오류가 PaLM 540B로 확장되었을 때 수정되는지를 분석하였습니다. 결과적으로, PaLM을 540B로 확장하면 62B 모델에서 발생하는 한 단계 누락 오류와 의미론적 이해 오류가 상당 부분 수정되는 것으로 확인되었습니다.
이러한 연구 결과를 종합하면, 사고의 연쇄 프롬프팅이 큰 규모의 언어 모델에서 복잡한 추론 문제를 풀기 위한 중요한 도구로 작용한다는 것을 알 수 있습니다. 연구자들은 이러한 기술을 통해 기계 학습 모델의 이해력과 성능을 개선하고, 더욱 다양한 문제를 해결할 수 있는 모델을 개발할 수 있을 것으로 기대합니다. 그러나 이 기술이 완벽하지는 않으며, 여전히 수정할 오류와 개선할 방법들이 존재합니다. 연구가 계속 진행되면서 사고의 연쇄 프롬프팅 기술이 더욱 발전할 것으로 예상됩니다.
References
