개괄
Affinity Propagtion(AP) 은 데이터 포인트 간 “message passing” 개념을 기반으로 하는 클러스터링 알고리즘이다.
k-means와 k-medoids 같은 클러스터링 알고리즘과 달리, AP는 알고리즘 실행 전에 클러스터의 개수를 요구하지 않는다.
k-medoids 와 유사하게, AP는 입력 셋에서 클러스터를 대표하는 데이터(exemplars)를 찾는 방식으로 클러스터링을 한다.

Affinity Propagation
K-means와 그 유사한 알고리즘의 주요 단점은 클러스터의 개수를 정하고 최초 대표 점들을 선정해야 한다는 점이다.
AP는 데이터 포인트 쌍 간의 유사도를 측정하여 입력값으로 사용하고, 동시에 모든 데이터 포인트를 잠재적인 대표 데이터로 여긴다.
좋은 품질의 대표점들과 해당 클러스터들이 나타날 때까지 데이터 포인트 간에 실제 값 메시지가 교환된다.
AP는 입력 값으로 두 개의 데이터 셋을 요구한다.
- 데이터 포인트들 간의 유사도 : 한 개의 데이터 포인트가 다른 점의 대표 점이 되는 데 얼마나 적합한 지를 나타내는 지표.
- 두 개의 점 간 유사도가 없으면 같은 클러스터에 속해있을 수 없으므로, 유사도는 생략되거나 \(-\infty\) 로 표현될 수 있다. (자기가 구현을 어떻게 하느냐에 따라 다름)
- 선호도(Preferences) : 각 데이터 포인트의 대표 점이 되기 위한 적합성을 나타내는 지표.
- 특정 데이터를 선호하게 할 수 있는 우선 정보가 있을 수 있다. 선호도를 통해 표현할 수 있다.
유사도와 선호도 모두 단일 대각 행렬(value가 대각선에 있고 나머지는 0)로 표현할 수 있다. 행렬 표현은 dense dataset에 사용하기 좋다. 점 간 연결이 드물 경우, 전체 n x n 행렬을 메모리에 저장하지 않고 연결된 점 간의 유사도 리스트를 유지하는 것이 더 실용적이다. ‘점 간 메시지 교환’은 행렬을 다루는 것과 동일하다. 이는 관점과 구현의 문제일 뿐이다.
AP는 수렴이 될 때까지 다음 이터레이션을 돈다. 각 이터레이션은 두 개의 message-passing step을 지닌다.
- 책임도(Responsibilities) 계산
- 책임도(Responsibility) r(i, k) 는 점 i의 다른 잠재적인 대표 점들을 고려하여 점 i의 대표점으로서 점 k 가 적합한지를 위한 누적된 증거를 반영한다. 책임도는 점 i 에서 후보 대표점 k로 전송된다.
- 가용도(Availabilities) 계산
- 가용도(Availability) a(i, k) 는 점 k가 대표점이 되어야 하는 다른 점들의 지원을 고려하여 대표점으로 k를 선택하는 것이 얼마나 적절한지에 대한 누적 증거를 반영한다. 가용도는 후보 대표점 k에서 점 i로 전송된다.
책임도와 가용도는 처음 0으로 세팅한다.
책임도는 다음과 같이 계산된다.
점 i와 점 k 사이의 유사도 값에서 점 i와 다른 후보 대표점 사이의 유사도 및 가용도 합에서 가장 큰 것을 뺀 것이다. 대표점에 얼마나 적합한 지 계산하는 논리 이면에는 초기 우선 선호도가 더 높으면 점수도 더 높지만, 스스로 좋은 후보라고 여기는 유사한 점이 있으면 책임도 점수는 떨어지기 때문에 이터레이션에서 하나가 결정될 때까지 둘 사이에서 경쟁이 벌어지는 것이다. \(s(i, k)\) 는 음의 거리로 정의되는 유사도이다. 특히 s(k, k) 는 특정 음수 값으로 사용자가 지정하는 데 이 값에 따라 클러스터 수가 달라진다. s(k, k) 가 커지면 자기 자신에 대한 유사도가 커져 클러스터 수가 늘어난다.
가용도를 계산할 때 각 후보가 좋은 대표점인지 여부를 입증하는 자료로 책임도를 사용한다.
a(i, k)는 자기에 대한 책임도 r(k, k)와 후보 대표점이 다른 점들로부터 받는 양수의 책임도의 합이다.
마지막으로 값이 변화하는 정도가 임계치 아래로 떨어지거나 최대 반복 횟수에 도달할 때 절차를 종료하기 위한 기준을 가질 수 있다. AP 절차를 통해 어느 지점에서든, 책임도(r)와 가용도(a) 행렬을 합하면 필요한 클러스터링 정보를 얻을 수 있다. 점 i의 대표점은 최대 r(i, k) + a(i, k)가 되는 k이다. 대표점들 집합을 필요로 한다면, 행렬의 주요 대각선을 스캔하면 된다. \(r(i, i) + a(i, i) > 0\) 이면 점 i가 대표점이다.
K-Means와 그 유사한 알고리즘에서 사전에 클러스터 수를 결정하는 것은 어려운 일이다. AP를 사용하면 명시적으로 지정할 필요는 없지만, 최적의 클러스터 수보다 많거나 적더라도 약간의 조정이 필요할 수 있다. 다행히, 선호도를 조정하는 것만으로 클러스터 수를 줄이거나 늘릴 수 있다.
선호도를 더 높은 값으로 설정하면 클러스터 수가 늘어날 것이다. 각 점이 대표점이 되는 적합성에 대해 더 확실해지기 때문이다.
반대로, 선호도를 낮게 설정하면 클러스터 수가 줄어들게 된다. 그러나 현 상황에 정확히 맞는 결과를 얻기 위해서는 선호도를 조정하는 몇 번의 실행이 필요할 수 있다.
Code
scikit-learn(==0.24.2)을 사용해서 간단히 코드로 알아보도록 하겠다.
from sklearn.datasets import make_blobs
from sklearn.cluster import AffinityPropagation
from sklearn.metrics import *
# 데이터를 만든다.
# 2차원의 점 3개를 임의로 정한다.
centers = [[1, 1], [-1, -1], [1, -1]]
# 위에서 정한 점을 중심으로 300개의 샘플을 만든다.
X, labels_true = make_blobs(n_samples=300, centers=centers, cluster_std=0.5, random_state=0)
model = AffinityPropagation(preference=-50).fit(X)
cluster_centers_indices = model.cluster_centers_indices_
labels = model.labels_
n_clusters_ = len(cluster_centers_indices)
print('Estimated number of clusters: %d' % n_clusters_)
print("Adjusted Rand Index: %0.3f" % adjusted_rand_score(labels_true, labels))
print("Adjusted Mutual Information: %0.3f" % adjusted_mutual_info_score(labels_true, labels))
print("Silhouette Coefficient: %0.3f" % silhouette_score(X, labels, metric='sqeuclidean'))
Adjusted Rand Index: 0.912
Adjusted Mutual Information: 0.871
Silhouette Coefficient: 0.753
입력 값이 어느 클러스터인지 예측할 땐 다음과 같이 사용한다.
# 입력 값의 클러스터 인덱스를 반환
model_index = model.predict([[0.5, 1]])
# 클러스터 중심 점
model.cluster_centers_[model_index]
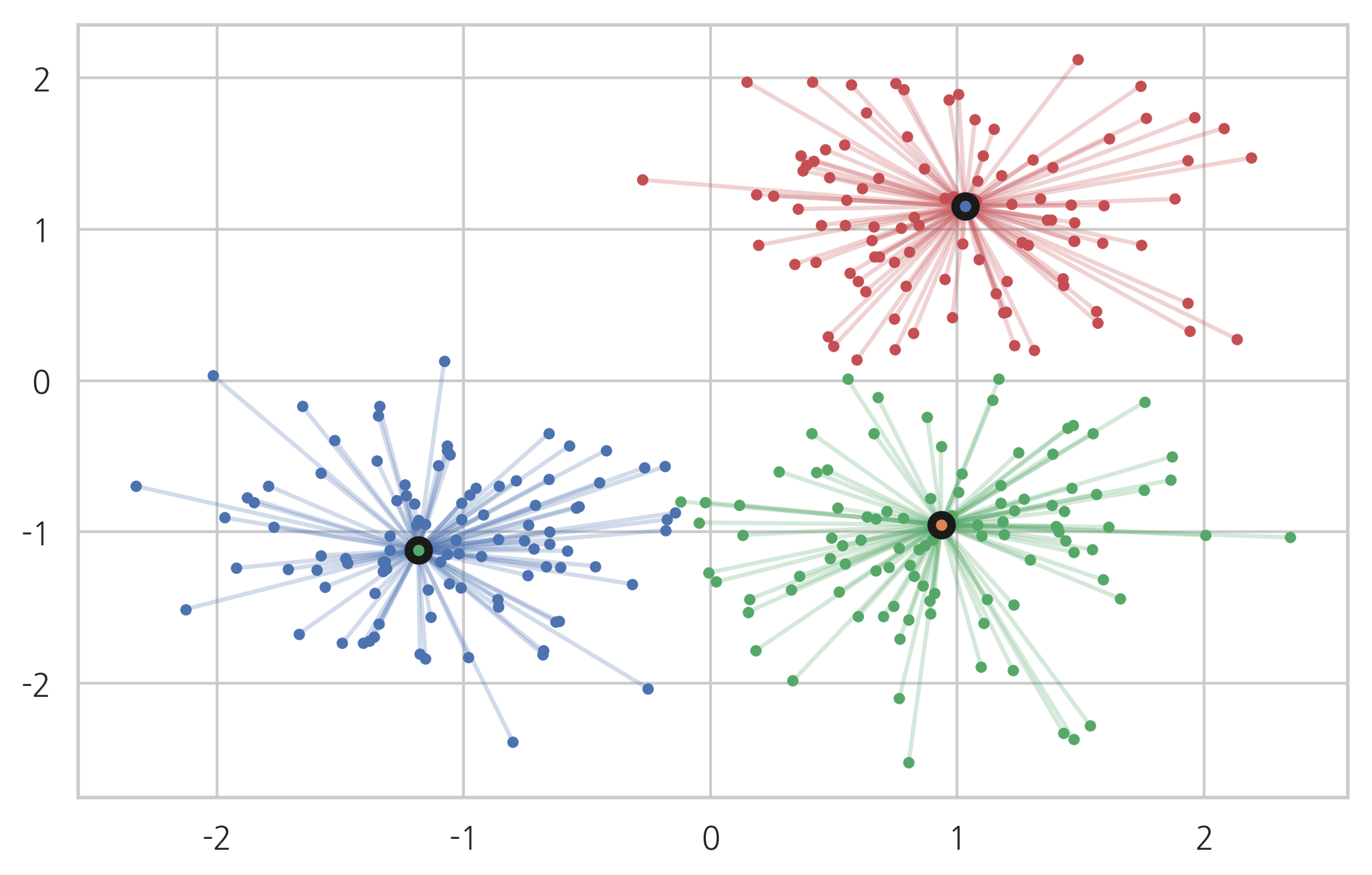
시각화해보면 다음과 같다.
from itertools import cycle
import matplotlib.pyplot as plt
colors = cycle('rgb')
for k, col in zip(range(n_clusters_), colors):
class_members = labels == k
cluster_center = X[cluster_centers_indices[k]]
plt.plot(X[class_members, 0], X[class_members, 1], col + '.')
for x in X[class_members]:
plt.plot([cluster_center[0], x[0]], [cluster_center[1], x[1]], col, alpha=0.25)
plt.plot(cluster_center[0], cluster_center[1], 'o', mec='k', mew=3, markersize=7)
plt.show()
References
