RNN 구조에 대해 설명하고 장단점을 살펴보도록 하겠습니다.

구조

RNN(Recurrent Neural Networks)은 아래 그림과 같은 구조를 지닌다.

• 히든 노드가 방향을 가진 엣지로 연결되어 순환구조를 이루는 인공신경망의 한 종류
• 음성, 문자 등 순차적(sequential)으로 등장하는 데이터 처리에 적합하다.
• 시퀀스의 길이에 무관하게 input과 output을 받아들일 수 있는 네트워크 구조이기 때문에 유연한 구조를 만들 수 있다!

• 위 그림은 RNN의 기본 구조
  • 녹색박스는 hidden state, 빨간 박스는 input x, 파란박스는 output y
  • 현재 상태의 hidden state ht는 직전 시점의 hidden state ht-1을 받아 갱신
  • hidden state의 활성함수는 비선형함수인 하이퍼볼릭탄젠트(tanh = sinh/cosh)
  • Tip) 활성함수로 비선형함수를 쓰는 이유

  선형함수인 h(x) = cx 를 활성함수로 사용한 3층 네트워크를 떠올려보세요. 이를 식으로 나타내면 y(x) = h(h(h(x))) 가 됩니다. 이 계산은 y(x) = c * c * c * x처럼 세번의 곱셈을 수행하지만 실은 y(x) = ax와 똑같은 식입니다. \(a=c^3\) 라고만 하면 끝이죠. 즉 hidden layer가 없는 네트워크로 표현할 수 있습니다. 그래서 층을 쌓는 혜택을 얻고 싶다면 활성함수로는 반드시 비선형 함수를 사용해야 합니다.

• RNN은 장기의존성(long-term dependency)에 문제가 있다.

• Exploding gradient problem : jacobian matrix(벡터를 벡터로 미분하면 나오는 행렬) 안의 값들이 클 때 activation 함수와 네트워크 파라미터 값에 따라 gradient가 지수 함수로 증가하여 문제가 되는 경우
  • exploding gradient는 쉽게 발견할 수 있다. 계속 커지면 gradient값들이 NaN이 될 것이고 결국 프로그램이 죽을 것이기 때문
  • (gradient clipping 기법) gradient 값들이 너무 크면 미리 정해준 적당한 값으로 잘라버리는 방법으로 이 문제를 해결할 수 있다. (Razvan, Tomas, & Yoshua, 2013)

• Vanishing gradient problem :

  

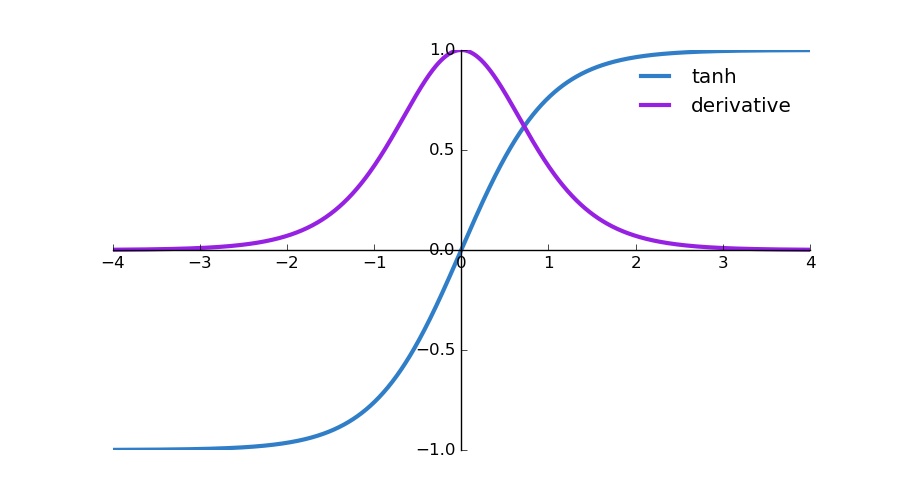
  • tanh나 sigmoid는 양쪽 끝에서 미분한 값이 0으로 수렴한다.
  • 이런 곳에서 그 뉴런들이 포화되었다고 말한다. 이런 뉴런들은 gradient가 거의 0이기 때문에 곱해지는 이전 layer의 gradient들도 0으로 수렴하게 만든다.
  • 따라서 행렬에 행렬에 작은 값들이 들어있고 여러 (t-k번) 행렬곱이 이루어지면 gradient는 지수 함수로 감소하고, 시간 스텝 몇 번만 지나도 사라져 버린다 (vanish!)
  • 즉, 시퀀스에서 여러 시간 스텝이 떨어진 곳에서는 gradient가 전달되지 못하고 먼 과거의 상태(state)는 현재 스텝의 학습에 아무 도움이 되지 못하게 된다.
• Vanishing 문제를 해결하려는 시도들
  • W 행렬 적당한 값으로 초기화
  • tanh, sigmoid 활성함수 대신 ReLU를 사용
    • ReLU는 0이하에 대해서는 0을 출력함으로써 활성화함수 역할을 하는 동시에 0 이상의 값들에 대해서는 미분값이 1이기 때문에 gradient값이 없어져버리는 일이 크게 줄어든다.

    

  • LSTM이나 GRU(Gated Recurrent Unit) 사용

    • LSTM

    • GRU

정리

RNN은 앞의 노드가 뒤의 노드로 순차적으로 연결되는 구조이기 때문에 시계열 데이터에 주로 쓰입니다. 자연어 처리도 흐름에 따른 문자열이기 때문에 RNN이 많이 쓰입니다. vanilla RNN에서 LSTM, GRU, seq2seq, attention, transformer, BERT까지 이어지는 흐름 상에서 시작에 불과하지만 그만큼 중요하다고 볼 수 있습니다.