- 교재 : Deep Reinforcement Learning Hands-On 2/E
- github : https://github.com/PacktPublishing/Deep-Reinforcement-Learning-Hands-On-Second-Edition
Intro
이번 챕터에서는 강화학습 방법 중 하나인 cross-entropy 에 대해 알아보겠습니다. 다른 방법들에 비해 덜 유명하지만, cross-entropy도 그만의 장점을 지닙니다.
- 매우 간단하다 –> 파이토치 코드가 100줄이 안 된다.
- 훌륭한 수렴성 –> 간단한 환경에서는 cross-entropy도 매우 잘 작동한다.
이번 챕터에서는 다음과 같은 내용을 다룰 예정입니다.
- cross-entropy의 실용적인 면을 다룬다.
- CartPole과 FrozenLake, 두 개의 Gym 환경에서 cross-entropy가 어떻게 작동하는지 알아본다.
- cross-entropy의 이론적 배경에 대해 다룬다.(Optional)
The taxonomy of RL methods
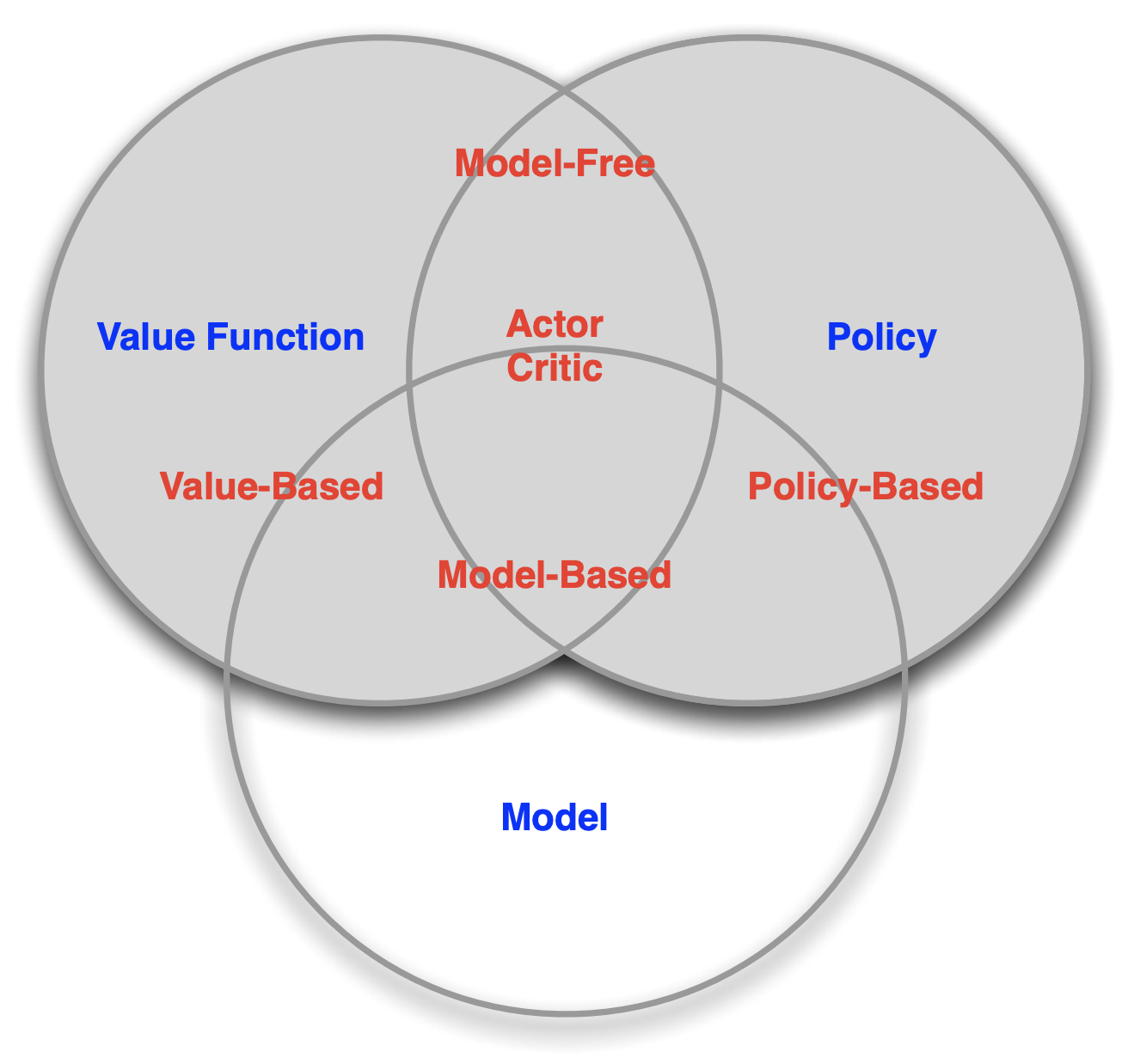
cross-entropy는 model-free, policy-based 방법입니다. 이 의미에 대해 알아보기 위해 강화학습을 나누는 여러 측면에 대해 먼저 얘기해보겠습니다.
- Model-free vs Model-based
- Value-based vs Policy-based
- On-policy vs Off-policy
Model-free vs Model-based
강화학습 알고리즘을 구분하는 주요 지점 중 하나는 에이전트가 환경의 모델에 접근(혹은 학습)을 할 수 있느냐입니다. 환경의 모델은 상태 전이와 보상을 예측하는 함수를 의미합니다.
Model-based 알고리즘은 환경의 모델을 지닌 알고리즘을 뜻합니다. Model-based 알고리즘은 계획(planning)이 가능하다는 장점을 지닙니다. 자신의 행동에 따라 환경이 어떻게 변할지 예측해서 최적의 행동을 계획하여 실행할 수 있다는 것입니다. 모델을 지닌다면 에이전트는 효율적으로 행동할 수 있습니다.
문제는 이 환경이 복잡할 경우에 환경의 모델을 알아내기 어렵거나 불가능하다는 점입니다. 모델이 환경을 제대로 반영하지 않는다면 이는 바로 에이전트의 오류로 이어지게 될 것입니다.
Model-based 알고리즘은 모델이 주어져 있는지 학습해야 하는지에 따라 또 구분이 가능합니다.
Model-free 알고리즘은 환경의 모델을 사용하지 않는 경우를 말하며, 관찰값과 행동을 바로 연결시킵니다. 현재 관찰값을 받아서 이를 기반으로 계산하고 그 결과로 행동을 하는 것입니다.
강화학습에서는 주로 model-free 알고리즘이 각광받고 있으며 우리가 아는 대부분의 유명한 알고리즘들(DQN, policy gradient, A2C, A3C 등)은 모두 model-free 입니다.
최근에는 두 알고리즘을 융합하는 시도도 하고 있습니다. 예를 들어, 딥마인드에서 내놓은 Imagination-Augmented Agents for Deep Reinforcement Learning 도 이러한 부류입니다. (22장에서 다룰 예정)
Policy-based vs Value-based
Policy-based 방법은 에이전트의 정책, 즉 에이전트가 모든 단계에서 수행해야 하는 작업을 직접 근사화합니다. 여기서 정책은 일반적으로 사용 가능한 작업에 대한 확률 분포로 표시됩니다.
반면, Value-based 방법의 에이전트는 액션의 확률 대신 가능한 모든 액션의 값을 계산하고 최상의 값을 가진 액션을 선택합니다. 그렇기 때문에 policy-based 방법과 달리 value-based 방법은 value function을 먼저 구하고 정책을 추정합니다.
On-policy vs Off-policy
off-policy는 action을 취하는 policy(behavior policy)와 improve하는 policy(target policy)를 다르게 취하는 것이고, on-policy는 두 policy가 동일한 경우를 뜻합니다.
cross-entropy는 on-policy에 해당합니다.
The cross-entropy method in practice
cross-entropy method의 핵심은 안좋은 에피소드는 버리고 좋은 에피소드에서 학습하는 것입니다. 학습 단계는 다음과 같습니다.
- 현재 모델과 환경으로 N번의 에피소드를 돌린다.
- 매 에피소드마다 총 보상을 계산하고 보상의 경계를 정한다. 보통 모든 보상의 백분위수를 사용한다.
- 경계 밖의 에피소드는 모두 버린다.
- 남은 에피소드를 기반으로 학습하고 결과를 비교한다.
- 만족스러운 결과가 나올 때까지 1~4의 스텝을 반복한다.
The cross-entropy method on CartPole
이 세션에서는 앞서 다룬 학습 단계를 기반으로 CartPole 환경에서 코드를 돌려보도록 하겠습니다. 전체 코드는 Chapter04/01_cartpole.py 에서 확인할 수 있습니다.
뉴럴넷은 간단한 구조를 사용하며 다음과 같은 하이퍼패러미터를 쓰고 있습니다.
- HIDDEN_SIZE = 128
- BATCH_SIZE = 16
- PERCENTILE = 70
PERCENTILE은 에피소드 필터링을 위한 백분위수입니다.
HIDDEN_SIZE = 128
BATCH_SIZE = 16
PERCENTILE = 70
class Net(nn.Module):
def __init__(self, obs_size, hidden_size, n_actions):
super(Net, self).__init__()
self.net = nn.Sequential(
nn.Linear(obs_size, hidden_size),
nn.ReLU(),
nn.Linear(hidden_size, n_actions)
)
def forward(self, x):
return self.net(x)
구조는 정말 간단합니다. 다만 마지막에 행동들에 대한 softmax를 계산하는게 보통인데 여기선 없습니다. 대신에, softmax와 cross-entropy를 하나의 수치적으로 더 안정적인 표현으로 결합하는 nn.CrossEntropyLoss 를 목적함수로 사용합니다. nn.CrossEntropyLoss 는 뉴럴넷에서 나온 정규화되지 않은 원시 값(logit)이 필요합니다. 단점은 뉴럴넷의 출력으로부터 확률을 얻기 위해서는 필요할 때마다 softmax를 적용해야 한다는 점입니다.
Episode = namedtuple('Episode', field_names=['reward', 'steps'])
EpisodeStep = namedtuple('EpisodeStep', field_names=['observation', 'action'])
collections.namedtuple로 2개의 helper class를 구성하였습니다.
- EpisodeStep : 에이전트가 에피소드에서 수행한 하나의 단계를 나타내며, 해당 환경에서 관찰한 내용과 에이전트가 완료한 액션을 저장합니다. 엘리트 에피소드의 episodestep를 학습데이터로 사용합니다.
- Episode : 할인되지 않은 총 보상과 EpisodeStep의 모음으로 구성된 단일 에피소드입니다.
우선 iterate_batches()를 살펴보면,
def iterate_batches(env, net, batch_size):
batch = [] # 배치사이즈만큼 Episode instance를 담을 리스트
episode_reward = 0.0 # 현재 에피소드의 reward counter
episode_steps = [] # episode_step을 담을 리스트
obs = env.reset() # 관찰값 초기화
sm = nn.Softmax(dim=1) # 뉴럴넷의 출력값을 action의 확률분포로 변환
이 함수는 gym의 환경, 뉴럴넷, 배치사이즈를 입력으로 받고 초기세팅을 합니다.
while True:
# PyTorch tensor로 변환
obs_v = torch.FloatTensor([obs])
# 뉴럴넷 -> softmax -> action 확률값
act_probs_v = sm(net(obs_v))
act_probs = act_probs_v.data.numpy()[0]
# 랜덤하게 action 선택
action = np.random.choice(len(act_probs), p=act_probs)
# action에 대한 환경의 response 받음.
next_obs, reward, is_done, _ = env.step(action)
episode_reward += reward
step = EpisodeStep(observation=obs, action=action)
episode_steps.append(step)
# 하나의 에피소드가 끝나면
if is_done:
# EpisodeSteps 모은 것을 하나의 에피소드 인스턴스로 저장한다.
e = Episode(reward=episode_reward, steps=episode_steps)
batch.append(e)
episode_reward = 0.0
episode_steps = []
next_obs = env.reset()
# 배치사이즈만큼 모이면 반환하고(generator) 초기화
if len(batch) == batch_size:
yield batch
batch = []
obs = next_obs
이제 학습을 위해 필터링하는 함수에 대해 알아보겠습니다. filter_batch()는 cross-entropy 메서드의 핵심입니다. 주어진 배치와 백분위수를 기준으로 경계가 되는 보상값을 계산하고 이를 필터링하는데 씁니다. 필터링된 에피소드는 학습에 사용됩니다.
def filter_batch(batch, percentile):
rewards = list(map(lambda s: s.reward, batch))
# 백분위수로 입력 배치의 경계 보상값 계산함.
reward_bound = np.percentile(rewards, percentile)
# 오직 monitoring 목적
reward_mean = float(np.mean(rewards))
train_obs = []
train_act = []
for reward, steps in batch:
# 보상이 경계값보다 작으면 생략한다.
if reward < reward_bound:
continue
# 각각 관찰값과 행동을 저장한다.
train_obs.extend(map(lambda step: step.observation, steps))
train_act.extend(map(lambda step: step.action, steps))
# 텐서로 변환
train_obs_v = torch.FloatTensor(train_obs)
train_act_v = torch.LongTensor(train_act)
return train_obs_v, train_act_v, reward_bound, reward_mean
학습 절차를 마무리하고 Tensorboard로 모니터링 해보도록 하겠습니다.
if __name__ == "__main__":
# 환경, 뉴럴넷, 목적함수, optimizer, 텐서보드 사용을 위한 summaryWriter의 인스턴스를 생성합니다.
env = gym.make("CartPole-v0")
# video를 만들고 싶으면 주석 풀기
#env = gym.wrappers.Monitor(env, directory="cartpole-mon", force=True)
obs_size = env.observation_space.shape[0]
n_actions = env.action_space.n
net = Net(obs_size, HIDDEN_SIZE, n_actions)
objective = nn.CrossEntropyLoss()
optimizer = optim.Adam(params=net.parameters(), lr=0.01)
writer = SummaryWriter(comment="-cartpole")
for iter_no, batch in enumerate(iterate_batches(
env, net, BATCH_SIZE)):
# filtering
obs_v, acts_v, reward_b, reward_m = \
filter_batch(batch, PERCENTILE)
optimizer.zero_grad()
action_scores_v = net(obs_v)
loss_v = objective(action_scores_v, acts_v)
loss_v.backward()
optimizer.step()
print("%d: loss=%.3f, reward_mean=%.1f, rw_bound=%.1f" % (
iter_no, loss_v.item(), reward_m, reward_b))
writer.add_scalar("loss", loss_v.item(), iter_no)
writer.add_scalar("reward_bound", reward_b, iter_no)
writer.add_scalar("reward_mean", reward_m, iter_no)
# 보상 평균값이 199보다 높으면 푼 것으로 하다.
if reward_m > 199:
print("Solved!")
break
writer.close()
결과를 보면 점차 보상의 경계값이 더 커지면서 loss값은 줄어드는 것을 확인할 수 있습니다.
0: loss=0.668, reward_mean=18.6, rw_bound=20.0
1: loss=0.676, reward_mean=17.4, rw_bound=14.5
2: loss=0.663, reward_mean=17.0, rw_bound=17.0
3: loss=0.664, reward_mean=20.8, rw_bound=21.5
4: loss=0.678, reward_mean=25.2, rw_bound=28.5
5: loss=0.673, reward_mean=26.8, rw_bound=37.5
...
34: loss=0.575, reward_mean=138.9, rw_bound=179.0
35: loss=0.560, reward_mean=139.1, rw_bound=174.0
36: loss=0.561, reward_mean=163.9, rw_bound=200.0
37: loss=0.540, reward_mean=159.2, rw_bound=198.0
38: loss=0.558, reward_mean=161.1, rw_bound=200.0
39: loss=0.550, reward_mean=178.7, rw_bound=200.0
40: loss=0.546, reward_mean=176.6, rw_bound=200.0
41: loss=0.537, reward_mean=182.4, rw_bound=200.0
42: loss=0.541, reward_mean=181.7, rw_bound=200.0
43: loss=0.533, reward_mean=193.8, rw_bound=200.0
44: loss=0.530, reward_mean=199.6, rw_bound=200.0
Solved!
위 결과는 텐서보드에서 그림으로 명확하게 볼 수 있습니다.
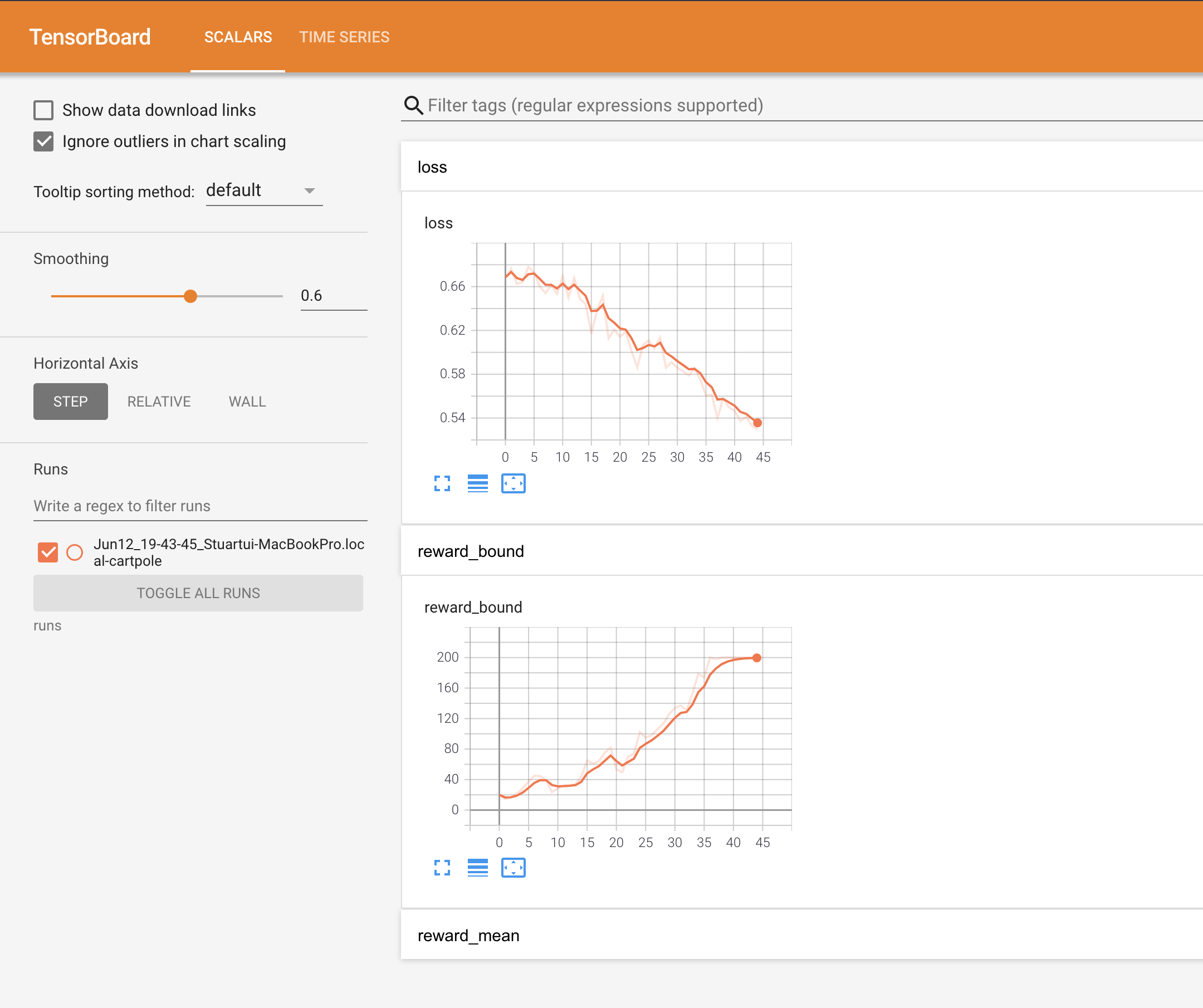
다음 세션에서는 또 다른 환경에서 cross-entropy를 다뤄보겠습니다.
The cross-entropy method on FrozenLake
FrozenLake 환경은 4 X 4 크기의 그리드월드이고 에이전트는 상하좌우로 움직일 수 있습니다. 좌상단에서 에이전트는 시작하고 우하단이 목표 지점입니다. 여기에 함정이 있는데 이 칸에 들어갈 경우 보상이 0이 되고 에피소드는 종료됩니다. 목표지점에 도달할 경우는 보상이 1이 되고 에피소드는 종료됩니다. 또 다른 조건은 환경의 이름처럼 이 환경에서는 미끄러질 수 있습니다. 그래서 에이전트가 왼쪽으로 가고자 해도 100%로 가는 것이 아니라 33% 확률로 가게 됩니다.
cartPole 예제에서 사용한 뉴럴넷을 그대로 쓰려는데 입력값에 차이가 있습니다. 뉴럴넷은 벡터 형태로 받기 원하면서 코드를 줄이기 위해 ObservationWrapper class를 상속한 DiscreteOneHotWrapper를 정의하였습니다.
class DiscreteOneHotWrapper(gym.ObservationWrapper):
def __init__(self, env):
super(DiscreteOneHotWrapper, self).__init__(env)
assert isinstance(env.observation_space,
gym.spaces.Discrete)
shape = (env.observation_space.n, )
self.observation_space = gym.spaces.Box(
0.0, 1.0, shape, dtype=np.float32)
def observation(self, observation):
res = np.copy(self.observation_space.low)
res[observation] = 1.0
return res
환경과 관찰값 형태만 바꾼 Chapter04/02_ frozenlake_naive.py 를 실행하면 앞선 경우와는 다른 결과가 나옵니다.
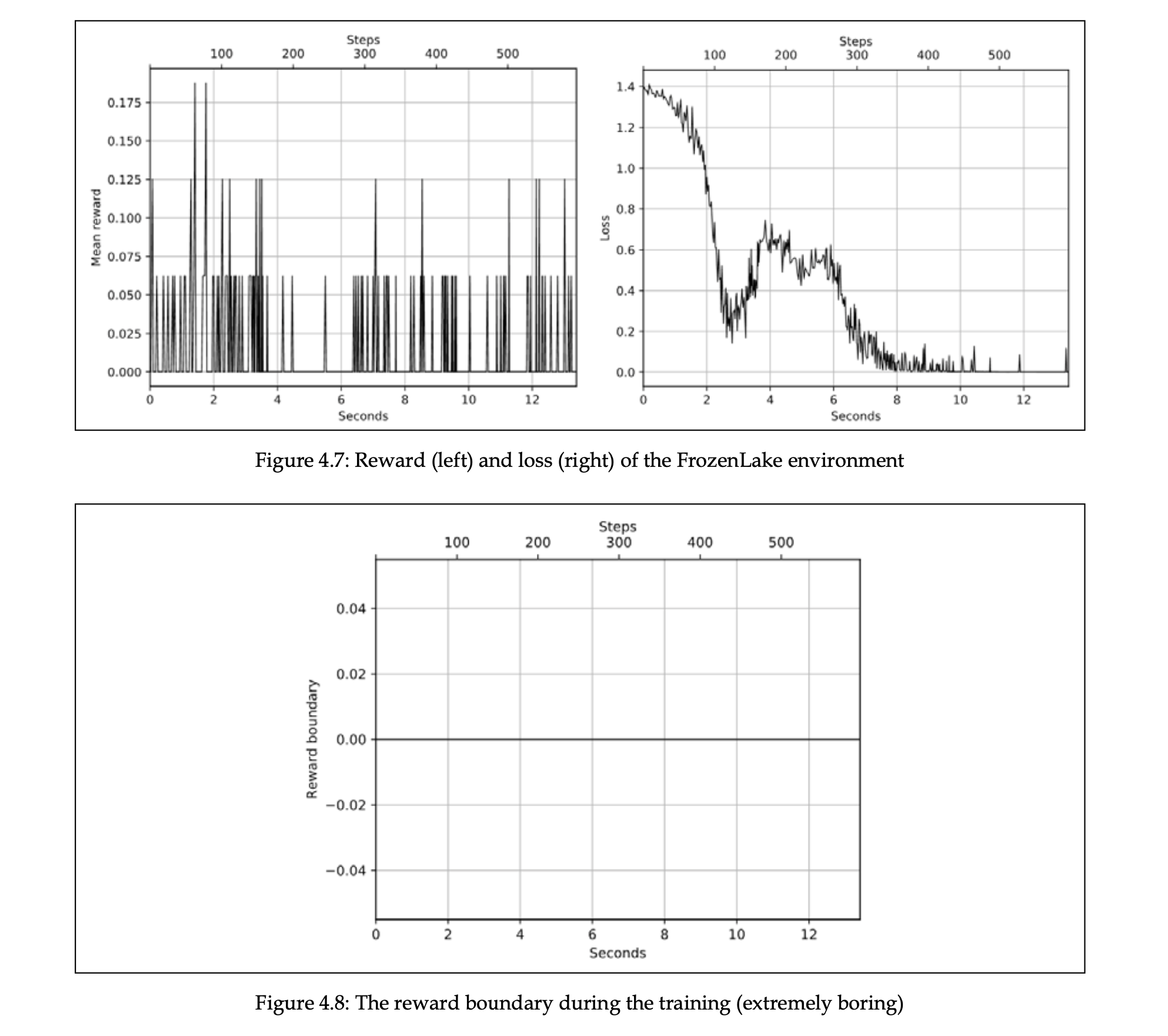
왜 그럴까요?
cartpole은 한 번 움직이기만 하면 보상을 줍니다. 오래 버티는 것이 목표이기 때문이죠. 그런데 frozenLake는 각 스텝마다 보상을 주는 것이 아니라 목표지점에 가야 1점을 주고 중간 중간 함정도 있습니다. 백분위수 기준으로 좋은 학습 데이터를 뽑을 수가 없으니 개선의 여지가 없습니다.
이 예제는 cross-entropy의 한계를 보여줍니다.
- 학습을 위해서, 에피소드는 유한해야 하고, 가급적이면 짧아야 한다.
- 좋은 에피소드와 나쁜 에피소드를 분리할 수 있을 정도로 학습 에피소드들의 총 보상은 충분한 분산을 가져야 한다.
- 에이전트가 성공했는지 실패했는지 중간 지시자가 없다.
Chapter04/03_frozenlake_tweaked.py 에서는 몇 개의 수정을 통해 cross-entropy로 frozenLake를 해결하고자 했습니다.
- batch size를 늘리기
- 보상에 discount factor 적용
- 좋은 에피소드는 오래 지니고 있기
- 학습률 줄이기
- 학습시간 늘리기
def filter_batch(batch, percentile):
# gamma 할인율
filter_fun = lambda s: s.reward * (GAMMA ** len(s.steps))
disc_rewards = list(map(filter_fun, batch))
reward_bound = np.percentile(disc_rewards, percentile)
train_obs = []
train_act = []
elite_batch = []
for example, discounted_reward in zip(batch, disc_rewards):
if discounted_reward > reward_bound:
train_obs.extend(map(lambda step: step.observation,
example.steps))
train_act.extend(map(lambda step: step.action,
example.steps))
elite_batch.append(example)
return elite_batch, train_obs, train_act, reward_bound
아래 메인 함수 내에도 변화가 있는데, full_batch를 통해서 좋은 에피소드는 오랫동안 가지고 있게 됩니다.
# main함수에서
full_batch = []
for iter_no, batch in enumerate(iterate_batches(
env, net, BATCH_SIZE)):
reward_mean = float(np.mean(list(map(
lambda s: s.reward, batch))))
full_batch, obs, acts, reward_bound = \
filter_batch(full_batch + batch, PERCENTILE)
if not full_batch:
continue
obs_v = torch.FloatTensor(obs)
acts_v = torch.LongTensor(acts)
full_batch = full_batch[-500:]
이 코드로 돌리면 다음과 같이 개선된 결과를 볼 수 있습니다.
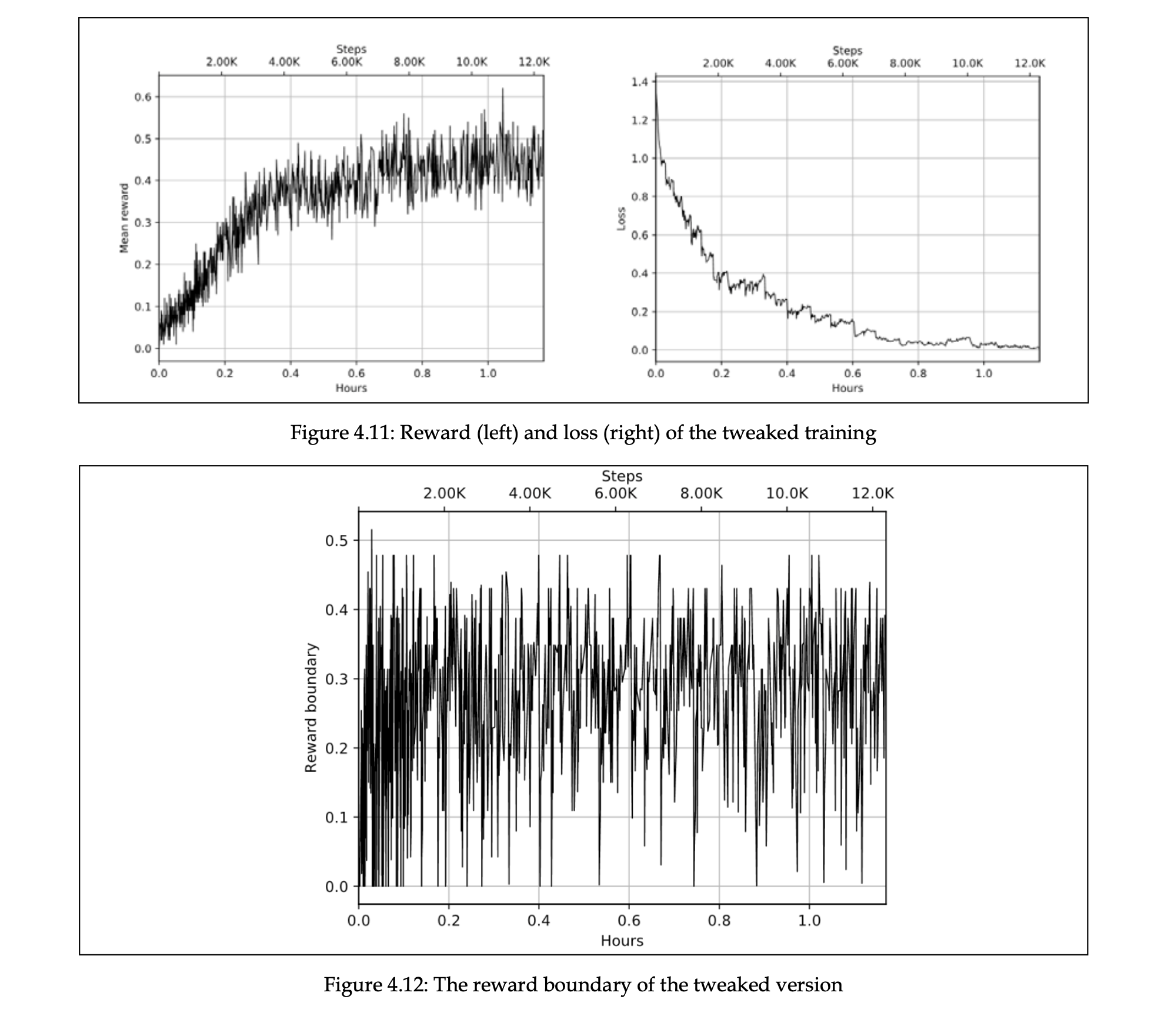
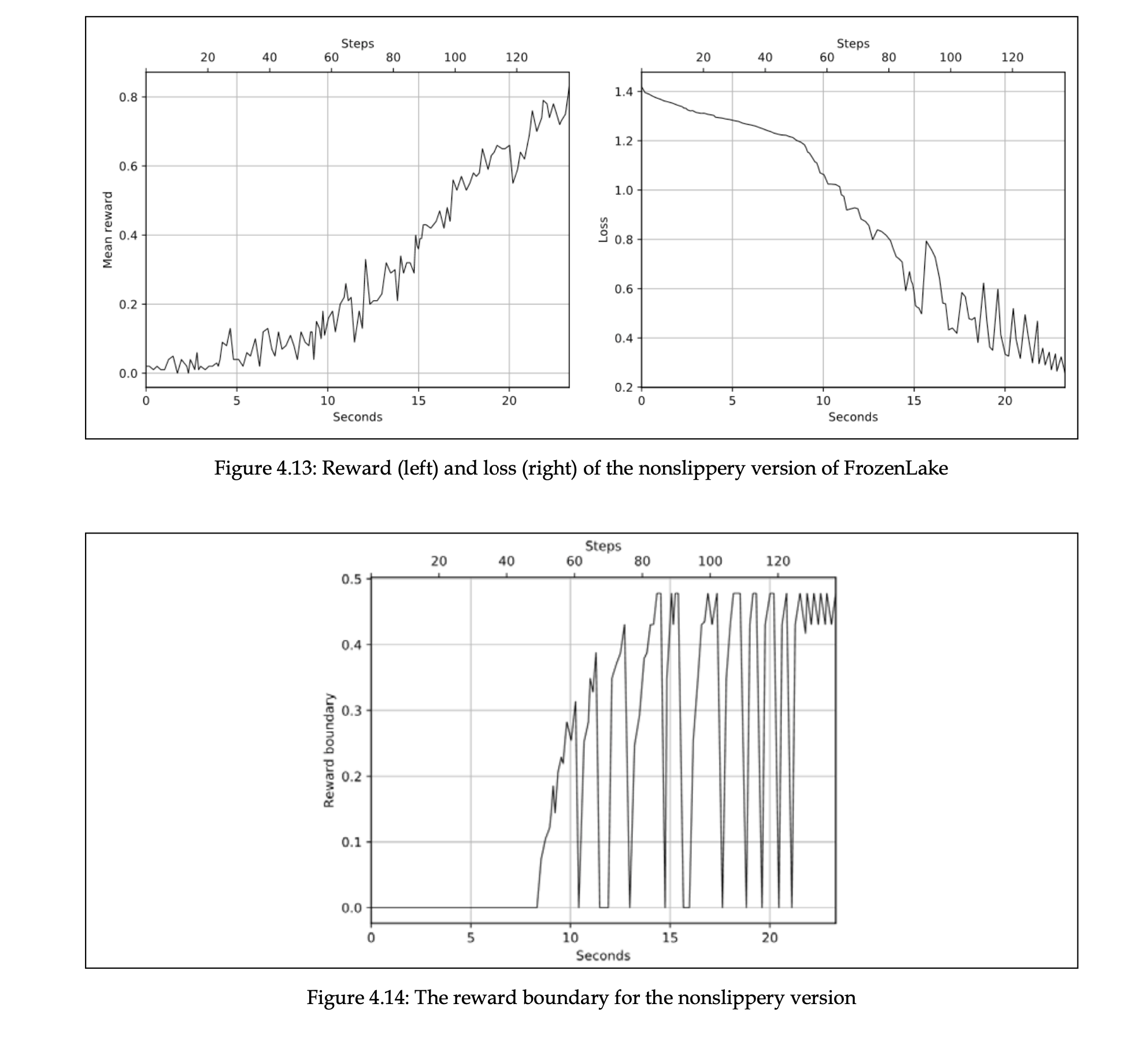
Chapter04/04_frozenlake_nonslippery.py 에서는 넘어짐 조건을 비활성화하여 실행합니다.
env = gym.envs.toy_text.frozen_lake.FrozenLakeEnv(is_slippery=False)
env.spec = gym.spec("FrozenLake-v0")
env = gym.wrappers.TimeLimit(env, max_episode_steps=100)
env = DiscreteOneHotWrapper(env)
이렇게 할 경우 120~140 배치 사이에 문제를 풀 수 있습니다.(제한된 목표 설정 하에)
rl_book_samples/Chapter04$ ./04_frozenlake_nonslippery.py
0: loss=1.379, reward_mean=0.010, reward_bound=0.000, batch=1
1: loss=1.375, reward_mean=0.010, reward_bound=0.000, batch=2
2: loss=1.359, reward_mean=0.010, reward_bound=0.000, batch=3
3: loss=1.361, reward_mean=0.010, reward_bound=0.000, batch=4
4: loss=1.355, reward_mean=0.000, reward_bound=0.000, batch=4
5: loss=1.342, reward_mean=0.010, reward_bound=0.000, batch=5
6: loss=1.353, reward_mean=0.020, reward_bound=0.000, batch=7
7: loss=1.351, reward_mean=0.040, reward_bound=0.000, batch=11
......
124: loss=0.484, reward_mean=0.680, reward_bound=0.000, batch=68
125: loss=0.373, reward_mean=0.710, reward_bound=0.430, batch=114
126: loss=0.305, reward_mean=0.690, reward_bound=0.478, batch=133
128: loss=0.413, reward_mean=0.790, reward_bound=0.478, batch=73
129: loss=0.297, reward_mean=0.810, reward_bound=0.478, batch=108
Solved!
The theoretical background of the cross-entropy method
보통은 이론적 배경이 앞에 나오는데 뒤에 배치된 이유는 책에서 이 부분을 옵션으로 여기고 있어서입니다.
cross-entropy method는 importance sampling theorem에 기초를 두고 있습니다. (다음은 importance sampling 수식입니다.)
RL에서 \(H(X)\) 는 policy \(x\)에 의해 얻어진 보상값이고, \(p(x)\) 는 모든 가능한 정책의 분포입니다. 모든 정책들을 뒤져가며 보상을 최대화하는 것이 아니라 두 확률 분포의 거리를 줄이기를 반복하면서 \(\frac{p(x) H(x)}{q(x)}\) 을 근사하는 방법을 찾고자 합니다. 두 확률 분포 간 거리는 Kullback-Leibler(KL) divergence로 계산합니다.
첫번째 텀이 엔트로피이고 \(p_2(x)\) 에 의존하지 않기 때문에 최소화할 때 생략가능합니다. 두번째 텀이 cross-entropy이고, 이는 딥러닝에서 가장 일반적인 최적화 목적함수입니다.
두 수식을 결합하여, \(q_0(x)=p(x)\) 에서 시작하여 매 단계마다 개선되는 반복 알고리즘을 얻을 수 있습니다. 다음과 같은 업데이트식을 통해 \(p(x)H(x)\) 를 근사할 수 있습니다.
아래 식은 이 장에서 다룬 RL 예제에서 크게 단순화할 수 있는 일반적인 교차 엔트로피 방법입니다. 먼저, \(H(x)\) 를 지시 함수로 대체하는데, 이는 에피소드에 대한 보상이 역치를 초과할 때 1이고 보상이 역치보다 작으면 0 이 됩니다. 정책 업데이트는 다음과 같습니다.
엄격하게 봤을 때 위 식은 정규화 조건을 빠뜨렸으나 우리 예제에서는 잘 작동합니다.
Summary
이번 장에서는 cross-entropy method의 실용적 쓰임새와 두 개의 환경에서 실행을 통해 cross-entropy의 장단점에 대해 알아보았습니다.
다음 챕터에서는 value-based method 중심으로 다뤄보도록 하겠습니다.
References
- Deep Reinforcement Learning Hands On 2/E Chapter 04 : The Cross-Entropy Method
- https://dreamgonfly.github.io/blog/rl-taxonomy/
- https://spinningup.openai.com/en/latest/spinningup/rl_intro2.html
