[Deep Reinforcement Learning Hands On 2/E] Chapter 11 : Policy Gradients - an Alternative

Intro

책의 3번째 파트 시작 장에 해당하는 이 장에서는 MDP 문제를 다루는 또 다른 방법인 policy gradient 에 대해 알아보겠습니다.

챕터 목표

pg 개괄, 동기, 그리고 q-learning과 비교한 강,약점을 다룬다.
간단한 policy gradient 방법인 REINFORCE 로 CartPole 예제를 다루면서 DQN 과 어떻게 다른지 비교해본다.

Values and policy

두 번째 파트에서 다룬 value iteration 과 Q-learning 의 중심 토픽은 상태의 value 혹은 (value, action) pair 였습니다. value 는 지금 상태(or 상태 & 행동)로부터 얻을 수 있는 총 보상의 할인된 값으로 정의됩니다. value 를 알면 매 단계에서의 에이전트의 결정은 간단하고 명백합니다. 가치의 관점에서 greedy 행동하면 됩니다. 이는 에피소드 끝에서 높은 총 보상을 보장합니다. 이러한 가치를 얻기 위해 벨만 방정식을 사용했습니다.

큐러닝에서처럼 가치가 어떻게 행동해야 할지 지시할 때, 가치는 정책을 실제로 정의한다고 말할 수 있습니다. 이를 공식으로 쓰면 다음과 같습니다.

\[\pi(s) = argmax_{a} Q(s,a)\]

정책과 가치의 관계는 명백해서 별도의 주체로서 정책을 강조하지 않고 대부분의 시간을 가치와 가치에 대한 정확한 근사 방법에 대해 이야기했습니다. 이러한 방식을 value-based method 라고 합니다. 이 방법과 대척점에 있는 것은 아니지만 다른 방법이 있습니다.

Why the policy-based method

value-based method 가 가치를 계산하고 나서 그에 따라 간접적으로 최고의 정책을 찾았다면 policy-based method 는 가치를 통해 정책을 찾는 것이 아니라 곧 바로 정책을 찾는 방식입니다. 정책 기반 학습이 왜 필요한지 살펴보겠습니다.

1. 정책은 우리가 강화학습 문제를 풀 때 찾고자 하는 것입니다.

에이전트가 관찰값을 가지고 있고 다음에 무엇을 할지 결정을 내려야 할 때, 가치나 행동이 아니라 정책이 필요합니다. 우리는 총 보상에 대해 신경 쓰지, 매 단계에서의 정확한 상태의 가치에는 관심이 없습니다.

큐러닝은 간접적으로 상태의 가치를 근사하고 최고의 대안을 찾으려고 하면서 정책 질문에 답하고자 하지만, 가치에 관심이 없다면 굳이 추가적인 일을 해야 할까요?

2. 많은 행동이 있는 환경 혹은 연속적인 행동 공간에서도 효과적입니다.

우리는 \(Q(s,a)\) 를 최대화하는 행동 a 를 찾는 최적화 문제를 풀어야 합니다. 몇 개의 행동을 가진 아타리 게임에서는 이것이 문제가 되지 않습니다. 모든 행동에 대해 가치를 근사하여 최고의 Q값을 갖는 행동을 선택하면 됩니다.

하지만 행동이 엄청 많거나 연속적이라면 가치를 계산하는 시간과 비용상 최적화 문제는 풀기 어려워질 것입니다. 이 경우에 가치보다는 정책을 직접 다루는 것이 현실 가능성이 높습니다.

3. 정책 기반 학습은 stochastic policy 학습이 가능합니다.

챕터 8에서 categorical DQN 의 에이전트는 기댓값이 대신에 Q-value의 분포를 사용해서 많은 이점을 누렸습니다. 네트워크가 내재된 확률 분포를 더 정확하게 잡아낼 수 있기 때문입니다. 정책 기반 학습에서 정책은 본질적으로 행동의 확률로 표현합니다.

Policy representation

앞서 정책은 행동의 확률로 표현된다고 했습니다.

그림으로 표현하면 다음 다이어그램에 나와 있습니다.

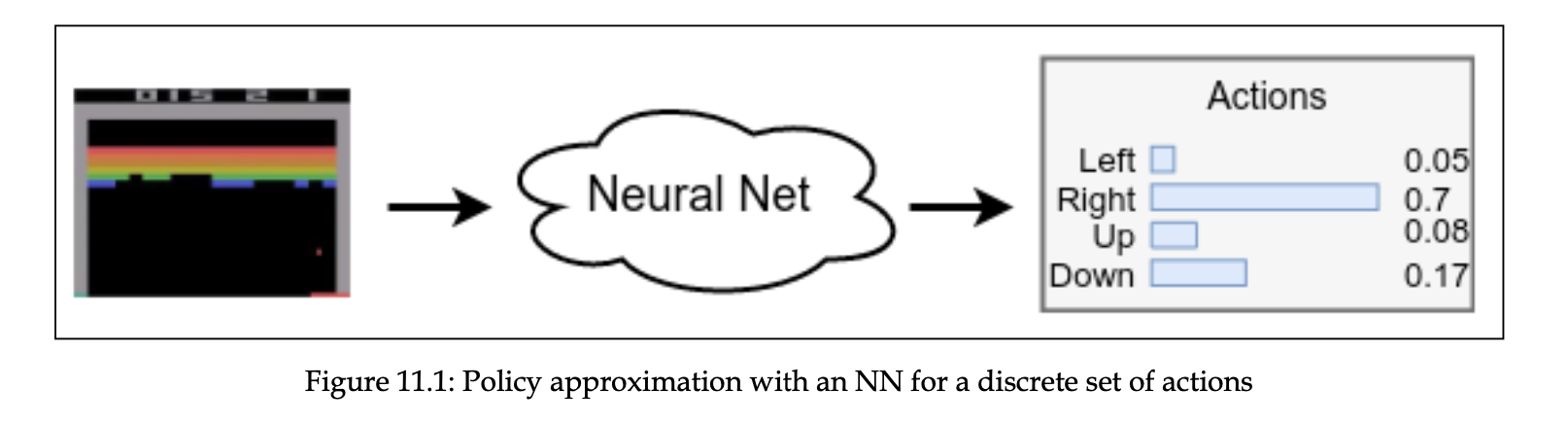
정책을 확률로 표현할 때 normalize 하는 가장 표준적인 방법은 softmax 를 쓰는 것입니다.

\[\pi(a|s, \theta) = \frac {exp(h(s,a, \theta))} {\sum_{b} exp(h(s,a,\theta))}\]

확률로 행동을 표현한 것은 smooth representation 이라는 이점을 가집니다.

뉴럴넷의 weights 를 조금 바꾸면 그 출력값도 바뀝니다. 많지 않은 행동을 가진 경우도 조금의 가중치 변화는 행동 선택에 있어서 큰 차이를 가져올 수 있습니다. 하지만 출력값이 확률 분포라면 가중치의 조그만 변화는 보통 출력값 분포의 작은 변화로 이어질 것입니다. 이는 gradient 최적화 방법들이 모델 개선을 위해 아주 조금씩 패러미터를 조정한다는 점에서 매우 좋은 속성입니다.

Policy gradients

policy gradients(pg) 는 목적 함수 \(J(\theta)\) 가 커지도록 패러미터를 업데이트하는 모든 방법입니다.

\[\theta_{t+1} = \theta_{t} + \alpha \triangledown J(\theta)\]

pg 의 목적 함수는 다음과 같이 정의할 수 있습니다.

\[\triangledown J \approx \mathbb{E}[Q(s,a)\triangledown \log \pi(a|s)]\]

식에 대한 증명보다는 식의 의미만 짚고 가겠습니다.

pg 는 축적된 총 보상의 관점에서 정책을 개선시키기 위해 네트워크의 패러미터를 바꾸는 방향을 정의합니다.
gradient의 scale 은 공식에서 Q(s,a) (즉, 행동의 가치)에 비례하고, gradient 자체는 취한 행동의 로그 확률의 gradient 와 같습니다. -> 좋은 총 보상을 주는 행동의 확률을 높이고 안 좋은 결과를 낳는 행동의 확률은 줄인다
기댓값(공식에서 \(\mathbb{E}\)) 은 여러 스텝에서의 gradient 를 평균내겠다는 의미입니다.

실용적인 관점에서 pg 는 다음 loss function 의 최적화를 수행하여 구현될 수 있습니다.
\(L = -Q(s,a) \log \pi(a|s)\)

마이너스 표시인 이유는 stochastic gradient descent(SGD) 할 때, 손실 함수는 최소화해야 하기 때문입니다.

The REINFORCE method

REINFORCE 는 pg 의 가장 기본적인 알고리즘입니다.
특정 정책에서 가능한 모든 trajectory (or path) 에 대한 total return 의 평균값을 구하고 그 평균값을 최대화하는 패러미터를 찾는 것이 기본 전략
Trajectory: \(\tau = (s_1, a_1, ... , s_t)\)
- 환경과 상호작용했을 때 얻어지는 state, action, (reward) 들의 시퀀스

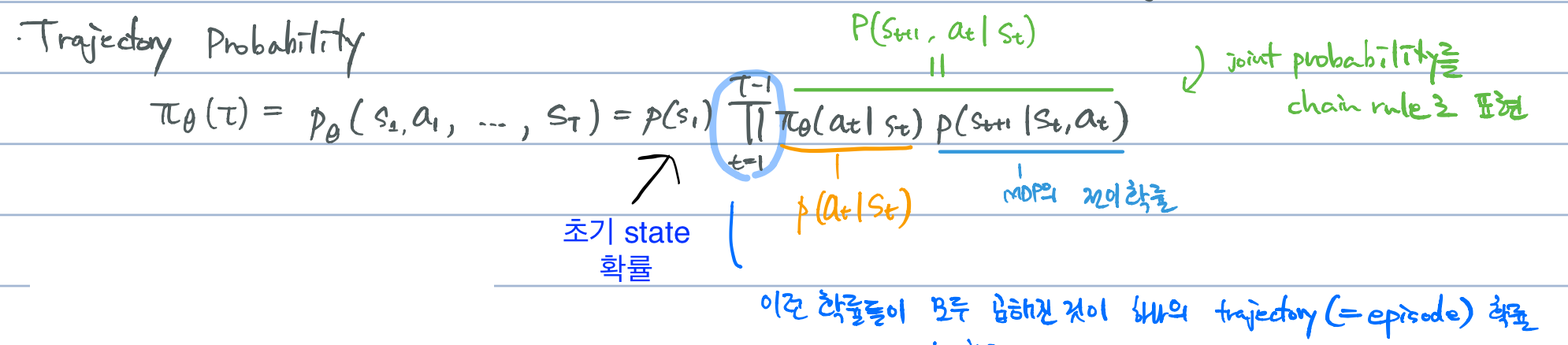
문제는 REINFORCE 가 이런 모든 transition 들의 total return 평균값을 구하는 것이 복잡하기 때문에 사용하는 트릭(?)들이 있습니다. 이걸 설명하는 것이 책의 취지와 맞지 않다고 생각해서 복잡한 계산이 없도록 간단한 방법으로 치환합니다.

cross-entropy 를 다루는 4장에서 몇 개 에피소드를 돌리면서 총 보상을 계산해보고 better-than-average 보상과 함께 학습했습니다. 이 학습 절차를 pg에도 적용하여 좋은 에피소드에는 Q(s,a)=1 을, 안 좋은 에피소드에는 Q(s,a)=0 을 부여하였습니다.

cross-entropy 와 다른 점은 단순히 0과 1을 쓰는 것 대신에 학습에 Q(s,a) 를 사용하는 것입니다.

무엇이 더 좋은가 보면, 일단 대답이 에피소드를 더 잘 정제해서 구분해줍니다. 예를 들어, 총 보상 10을 가진 에피소드의 transitions 은 보상 1을 가진 에피소드로부터 나온 transitions 보다 더 gradient 에 기여해야 합니다.

두 번째 이유는 에피소드 초반에 좋은 행동들의 확률을 높이고 에피소드 끝에 가까운 행동을 줄이기 위함입니다. 왜냐하면 Q(s,a)는 discounting factor 를 포함하고, 더 긴 행동 시퀀스에 대한 불확실성이 자동적으로 고려되기 때문입니다. REINFORCE 는 다음과 같이 진행됩니다.

임의의 가중치로 네트워크를 초기화
N 개의 전체 에피소드를 수행하여 transition (s, a, r, s’) 을 저장
모든 에피소드(k), 매 단계(t)마다, 다음 스텝의 할인된 총 보상을 계산: \(Q_{k,t} = \sum_{i=0} \gamma^{i} r_i\)
모든 transitions 에 대해 손실 함수 계산: \(L = - \sum_{k,t} \log(\pi(s_{k,t}, a_{k,t}))\)
loss를 최소하는 방향으로 가중치 업데이트(SGD 수행)
수렴할 때까지 step 2부터 반복

REINFORCE 는 큐러닝과 몇몇 중요한 측면에서 다른 면을 보입니다.

명백한 탐험이 없어도 된다.
- 큐러닝에서는 greedy 행동을 하면서도 탐험을 하기 위해 epsilon-greedy 전략을 사용했다. REINFORCE 에서는 확률론적이기 때문에 탐험이 자동적으로 수행된다. 시작할 때, 네트워크는 임의의 가중치로 초기화되고 그것은 uniform probability distribution 을 반환한다. 이 분포는 임의의 행동과 부합한다.
replay buffer 를 사용하지 않는다.
- policy gradient 는 on-policy 에 해당한다. 이는 이전 정책에서 나온 데이터에선 학습할 수 없다는 의미다. 여기에는 장단점이 있다. 좋은 점은 이러한 방법들은 보통 수렴이 빠르다는 점이다. 단점은 off-policy 보다 환경과의 상호작용을 더 요구한다는 점이다.
target network 를 필요로 하지 않는다.
- Q값을 사용하지만 Q값은 환경에서의 경험으로부터 얻어진다. DQN 에서는 Q 값 근사에서 그 상관관계를 깨기 위해 target network 를 사용했지만 REINFORCE 에서는 근사를 하지 않는다. (다만 다음 챕터에서 pg 에서 target network 트릭을 사용하면 유용하다는 점을 볼 수 있긴 하다.)

The CartPole example

REINFORCE 구현 코드를 익숙한 CartPole 환경에서 먼저 다뤄보도록 하겠습니다. 전체 코드는 Chapter11/02_cartpole_reinforce.py 입니다.

코드에 설명을 한 번에 달았습니다.

#!/usr/bin/env python3
import gym
import ptan
import numpy as np
from tensorboardX import SummaryWriter

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim

# hyperparameters settings
GAMMA = 0.99
LEARNING_RATE = 0.01
# 학습에서 사용할 완전한 에피소드 개수
EPISODES_TO_TRAIN = 4


class PGN(nn.Module):
    '''
    Policy Gradient Network
    dqn 코드와 다를 게 없다. 
    이론상으로 PGN 은 확률값을 반환해야 하지만 코드를 보면 그렇지 않다. 
    출력값에 softmax의 비선형성을 적용하지 않았다.
    이 부분은 PGN의 출력값을 처리하는 log_softmax 함수가 출력값을 softmax 하여 
    로그 계산하는 것을 한번에 하기 때문입니다.
    이 계산 방법이 수치적으로 더 안정되어 있어서 이렇게 사용한다.
    '''
    def __init__(self, input_size, n_actions):
        super(PGN, self).__init__()

        self.net = nn.Sequential(
            nn.Linear(input_size, 128),
            nn.ReLU(),
            nn.Linear(128, n_actions)
        )

    def forward(self, x):
        return self.net(x)


def calc_qvals(rewards):
    '''
    이 함수는 약간 트릭이 있다. 
    rewards 라는 모든 에피소드의 보상 목록을 받아서
    매 스텝마다 할인된 총 보상을 계산해야 한다. 
    효율적으로 진행하기 위해 지역적인 보상 목록의 마지막에서 계산했다.
    실제로, 에피소드 마지막 스텝은 지역 보상과 동일한 총 보상을 가질 것이다. 
    마지막 직전 스텝은  r_{t-1} + \gamma r_t 총 보상을 가질 것이다.
    '''
    res = []
    sum_r = 0.0
    for r in reversed(rewards):
        # sum_r 은 단계별 할인된 총 보상(local reward)
        sum_r *= GAMMA
        sum_r += r
        res.append(sum_r)
    return list(reversed(res))


if __name__ == "__main__":
    # 환경 설정
    env = gym.make("CartPole-v0")
    # SummaryWriter instance 생성
    writer = SummaryWriter(comment="-cartpole-reinforce")

    # PGN
    net = PGN(input_size=env.observation_space.shape[0], n_actions=env.action_space.n)
    print(net)

    '''ptan.agent.PolicyAgent는 모든 관찰값에 대한 행동을 결정한다. 
    PGN은 행동의 확률값을 정책으로 반환한다.
    취할 행동을 선택하기 위해 agent 는 pgn으로부터 확률값을 받아 해당 확률분포로부터 random sampling 을 수행한다.

    DQN의 경우 첫 번째 행동의 Q값(net 출력값)이 0.4, 두 번째 행동의 Q값이 0.5 면 무조건 두 번째 행동을 선택한다.
    PGN의 경우는 40%의 확률로 첫 번째 행동을, 50%의 확률로 두 번째 행동을 선택한다.

    다만, 현재 코드에선 두번째 행동을 100% 선택하는데 이는 첫 번째 행동에 대해 확률 0, 두번째 행동에 대해 확률 1을 반환하기 때문

    * PolicyAgent 는 내부적으로 확률값(from PGN)으로 NumPy 의 random.choice function 을 호출한다.
    * preprocessor=ptan.agent.float32_preprocessor
        - Gym의 CartPole env 는 float64 타입으로 관찰값을 주는데, PyTorch 는 float32 를 요구하기 때문에 전처리한 것이다.
    * apply_softmax 는 네트워크 출력값을 확률로 바꾸는 작업을 먼저 하라는 의미
    '''
    agent = ptan.agent.PolicyAgent(net, preprocessor=ptan.agent.float32_preprocessor,
                                   apply_softmax=True)
    '''
    # ExperienceSourceFirstLast
    주어진 환경에서 (state, action, reward, last_state) objects list로 제공
    full subtrajectories 가 아니라 n step 상황에서 첫번째(현재 스텝)와 마지막 스텝의 정보만 반환하는 특징
    
    - state: 현재 상태
    - action: 현재 상태에서 수행된 동작
    - reward: 현재 상태에서 n-step 을 보고 계산한 할인된 보상
    - last_state: 행동을 취하고 나온 상태(마지막이면 None)
    '''
    exp_source = ptan.experience.ExperienceSourceFirstLast(env, agent, gamma=GAMMA)

    # Adam Optimizer
    optimizer = optim.Adam(net.parameters(), lr=LEARNING_RATE)

    # variables for reporting
    # 보상 목록
    total_rewards = []
    step_idx = 0
    # 끝난 에피소드 개수
    done_episodes = 0

    # variables for gathering the training data
    batch_episodes = 0
    # batch_states, batch_actions 는 가장 최근 학습에서 본 states와 actions 담고 있는 리스트
    # batch_qvals: 에피소드 끝에 calc_qvals function 사용해서 local rewards 를 가지고 할인된 총 보상을 계산하는데 그 결과값을 batch_qvals 에 담는다.
    batch_states, batch_actions, batch_qvals = [], [], []
    # cur_rewards 는 진행 중인 에피소드의 local reward 를 담은 리스트
    cur_rewards = []

    for step_idx, exp in enumerate(exp_source):
        batch_states.append(exp.state)
        batch_actions.append(int(exp.action))
        cur_rewards.append(exp.reward)

        # 에피소드 마지막엔 None
        if exp.last_state is None:
            # local rewards 로 할인된 총 보상 계산
            batch_qvals.extend(calc_qvals(cur_rewards))
            cur_rewards.clear()
            batch_episodes += 1

        # 에피소드 마지막이면 수행하는 학습 절차
        # 현재 학습 진행 상황 보고
        # handle new rewards
        new_rewards = exp_source.pop_total_rewards()
        if new_rewards:
            # 완료한 에피소드 개수 증가
            done_episodes += 1
            reward = new_rewards[0]
            total_rewards.append(reward)
            # 최근 100개에 대한 보상들의 평균값을 사용
            mean_rewards = float(np.mean(total_rewards[-100:]))
            print("%d: reward: %6.2f, mean_100: %6.2f, episodes: %d" % (
                step_idx, reward, mean_rewards, done_episodes))
            writer.add_scalar("reward", reward, step_idx)
            writer.add_scalar("reward_100", mean_rewards, step_idx)
            writer.add_scalar("episodes", done_episodes, step_idx)
            # 평균 보상이 195보다 크면 문제 풀었다고 간주
            if mean_rewards > 195:
                print("Solved in %d steps and %d episodes!" % (step_idx, done_episodes))
                break

        if batch_episodes < EPISODES_TO_TRAIN:
            continue
        
        # 초기화 및 torch form 으로 변경
        optimizer.zero_grad()
        states_v = torch.FloatTensor(batch_states)
        batch_actions_t = torch.LongTensor(batch_actions)
        batch_qvals_v = torch.FloatTensor(batch_qvals)

        # net(PGN)의 출력값은 log_softmax() 을 통해 확률값으로 계산된다.
        logits_v = net(states_v)
        log_prob_v = F.log_softmax(logits_v, dim=1)
        # 행동들로부터 log probabilities 를 선택하여 q value로 scaling
        log_prob_actions_v = batch_qvals_v * log_prob_v[range(len(batch_states)), batch_actions_t]
        # 마이너스 붙이면 loss 는 줄여야, policy gradient는 최대화해야 정책을 개선할 수 있다.
        loss_v = -log_prob_actions_v.mean()

        loss_v.backward()
        optimizer.step()

        batch_episodes = 0
        batch_states.clear()
        batch_actions.clear()
        batch_qvals.clear()

    writer.close()

Results

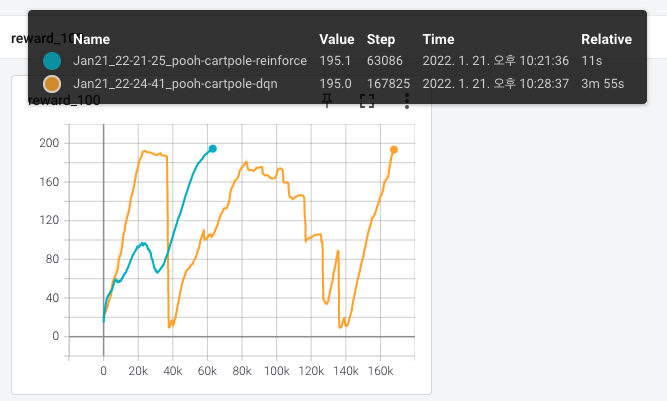
REINFORCE와 거의 동일한 hyperparameters 를 가지고 DQN으로 CartPole을 풀었을 때는 167,825 steps, 2,012 episodes 에 문제가 풀렸습니다. (Chapter11/01_cartpole_dqn.py)

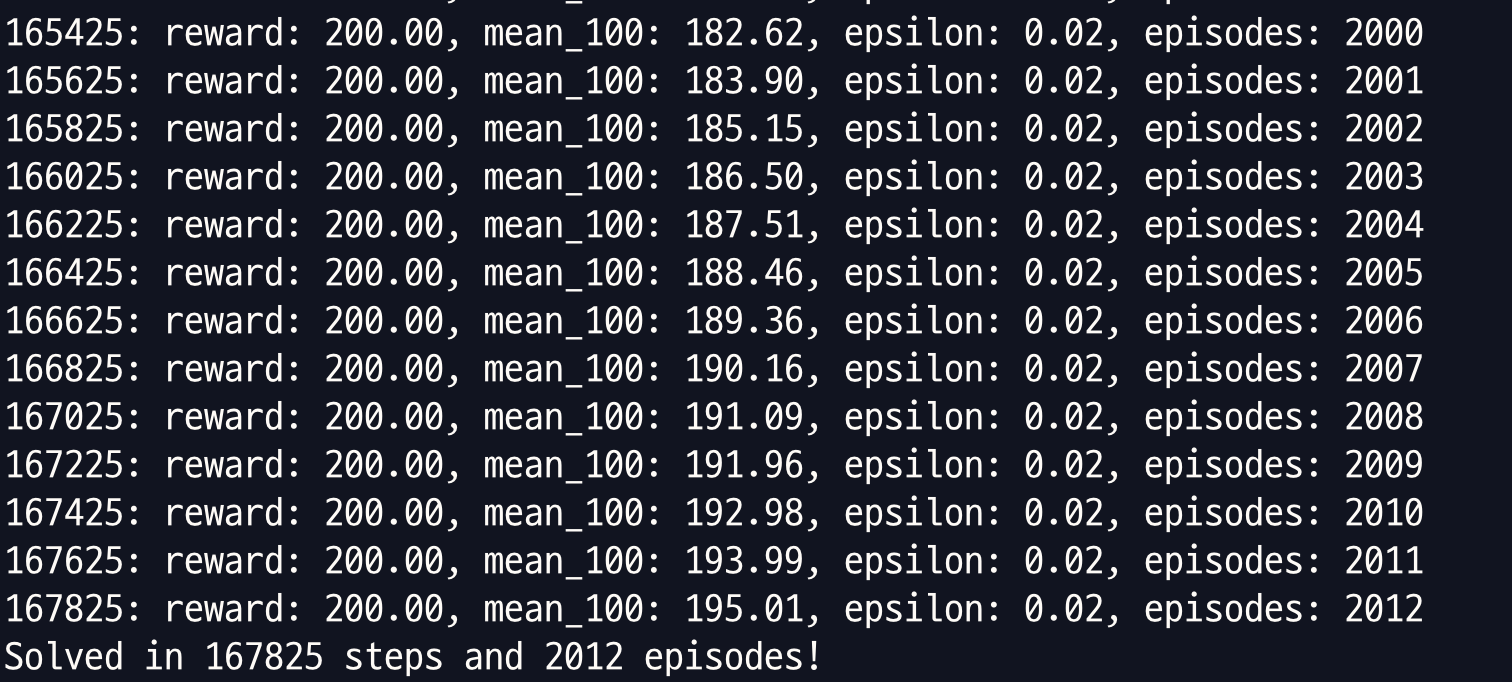
Chapter11/02_cartpole_reinforce.py 를 돌리면 다음과 같이 나옵니다.

dqn 과 비교해봤을 때 REINFORCE 가 훨씬 빨리 학습을 끝냈습니다. 이게 제가 돌린건데 dqn은 예상보다 더 헤맸고 REINFORCE 는 예상보다 빨리 풀은 결과인 것 같습니다. dqn은 거의 4분인데 REINFORCE는 11초네요.

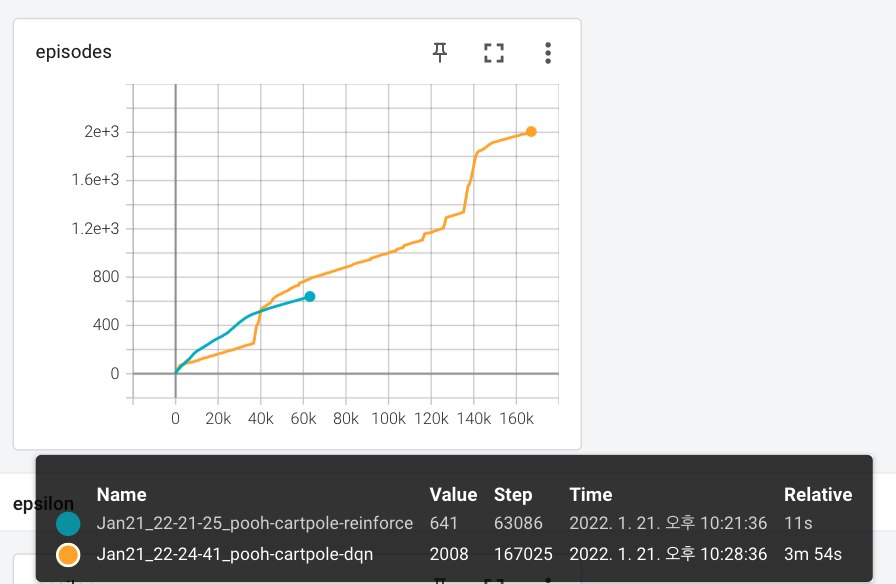
아래는 두 모델의 최근 100개 스텝의 보상 평균이 어떻게 변화했는지입니다.

Policy-based vs value-based methods

두 방법을 비교해보겠습니다.

항목	policy-based	value-based
정책 추구	직접적으로 정책을 최적화	간접적으로 최적화. 가치를 먼저 계산하고 이 가치에 기반한 정책을 제공
on/off	on-policy 이며 환경으로부터 새로운 샘플을 원함	on, off policy 둘 다 있고, off-policy의 경우 이전 데이터에서도 학습 가능
sample-efficiency	low	high. sample-efficiency 가 계산적으로 더 효율적이라는 말은 아님. 이는 거의 반대
수렴	대부분 수렴이 더 잘 되지만 global optimum 으로 수렴 보장 X	일부 global optimum 으로 수렴 보장

완전히 무엇이 나은 선택지다 라고 말할 수 없다는 것을 알 수 있습니다. 두 방법의 특징을 파악하여 상황에 맞게 쓰는 것이 중요합니다.

다음 섹션에서는 REINFORCE 방법의 한계와 이를 극복하는 방법, pg를 pong game에 적용하는 내용에 대해 소개하도록 하겠습니다.

REINFORCE issues

1. Full episodes are required

학습을 위해 완전한 에피소드가 필요하고 에피소드가 많을수록 성능이 올라갑니다. CartPole 같이 잘 정리되어 있고 짧은 에피소드로 구성되어 있으면 문제가 없지만 Pong 같이 에피소드마다 수백, 수천 프레임을 지속하는 경우는 문제가 될 수 있습니다.

학습 관점에서는 학습 배치가 커져야 해서 문제고, sample efficiency 관점에서는 환경과 더 많이 상호작용해야 한다는 문제가 있습니다.

완전한 에피소드가 필요한 이유는 가능한 한 정확한 Q-estimation 을 하기 위함입니다. DQN 에서는 할인된 보상의 정확한 값을 1-step 벨만 방정식( \(Q(s,a) = r_a + \gamma V(s')\) )을 이용해서 추정치로 대체할 수 있습니다. pg 의 경우 V(s) 나 Q(s,a) 가 없어서 DQN처럼 할 수가 없습니다.

이를 극복하기 위한 방법이 두 가지 있습니다.

Actor-Critic method
- 네트워크에 V(s) 를 추정하도록 만든 후에 이를 Q를 얻는 데 사용한다.
- 다음 챕터에서 다룰 예정이고, 인기가 많다.
Bellman equation, unrolling N steps ahead
- 벨만 방정식을 사용하여 N 스텝 앞서 보는 방식
- \(\gamma < 1\) 일 때, 가치의 기여도가 감소한다는 사실을 효과적으로 이용
  - \(\gamma = 0.9\) 일 때, 10 step에서 value coefficient 는 \(0.9^{10}=0.35\), 50 step 에서는 0.00515 이다.

2. High gradients variance

\[\triangledown J \approx \mathbb{E}[Q(s,a)\triangledown \log \pi(a|s)]\]

pg 의 공식에서 할인된 보상에 비례하는 gradient 를 발견할 수 있습니다. 보상의 범위는 굉장히 환경에 의존적입니다.

예를 들어, CartPole 환경에서 막대기를 수직으로 유지만 하면 매 timestamp 마다 1점을 보상으로 받습니다. 5 스텝을 버틴 것과 100 스텝을 버틴 것은 (할인 고려 안하면) 보상으로 치면 20배가 차이가 납니다. 운 좋은 에피소드 하나가 최종 gradient 를 지배할 수도 있기 때문에 이러한 큰 차이는 학습 dynamics에 심각한 영향을 끼칠 수 있습니다.

수학적인 관점에서 pg는 큰 분산을 가졌습니다. 복잡한 환경에서 이에 대해 대처하지 않으면 학습 프로세스가 불안정해 질 수 있습니다. 보통 이 경우 Q에서 baseline 이라는 값을 빼는 것이 해결 방법입니다. baseline에 사용할 수 있는 옵션은 다음과 같습니다.

일반적으로 할인된 보상의 평균값(상수)
할인된 보상의 이동평균
상태값 V(s)

3. Exploration

정책이 확률 분포로 표현된다 해도, 에이전트가 지역적으로 최적화된 정책에 수렴되거나 환경 탐험을 그만 둘 여지는 충분합니다. DQN 의 경우 epsilon-greedy action selection 방법을 썼는데 pg 에서도 쓸 수 있습니다. pg에서는 이를 entropy bonus 라고 부릅니다.

정보이론에서 엔트로피는 불확실성의 정도입니다. 어떤 정책을 적용했을 때, 엔트로피는 에이전트가 그 행동을 했을 때 얼마나 불확실한지 보여줍니다. 수학 표기로 정책의 엔트로피는 다음과 같이 정의됩니다.

\[H(\pi) = - \sum \pi(a|s) log \pi(a|s)\]

엔트로피 값은 항상 0 이상이고, 정책이 균일할 때, 즉 모든 행동이 동일한 확률을 가질 때 단일한 최대값을 가집니다.

엔트로피는 정책이 하나의 행동에 대해 1 이고 나머지에 대해 0 일 때, 최소값이 됩니다. local minimum 에 에이전트가 빠지는 것을 방지하기 위해 loss function 에서 엔트로피를 빼고, 에이전트가 취한 행동에 과한 확실성을 보이면 제재를 가했습니다.

4. Correlation between samples

단일 에피소드에 있는 학습 샘플들은 보통 강한 상관관계를 가지고 이는 SGD 학습에 안 좋습니다.

DQN 의 경우 큰 replay buffer 를 사용하는 것으로 문제를 해결합니다. pg가 on-policy 이기 때문에 pg 에는 적용할 수 없습니다. 오래된 데이터와 오래된 정책을 사용하면 현재가 아니라 오래된 정책을 위한 pg 를 얻게 될 것입니다.

이 문제를 해결하기 위해서는 보통 병렬적인(parallel) 환경을 사용합니다. 하나의 환경과만 상호작용하는 게 아니라, 여러 개의 환경을 사용하고 그에 따른 transition 들을 학습 데이터로 활용하는 것입니다.

Policy gradient methods on CartPole

최근에는 vanilla policy gradient 를 사용하는 사람은 거의 없지만 vanilla model 이 가지는 중요한 개념과 pg 성능 체크를 하는 척도를 살펴보기 위해 구현해보도록 하겠습니다.

Implemenation

처음에는 CartPole 을 대상으로 하고 다음은 Pong game으로 해보겠습니다.

#!/usr/bin/env python3
import gym
import ptan
import numpy as np
from tensorboardX import SummaryWriter
from typing import Optional

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim

# hyperparameters settings
GAMMA = 0.99
LEARNING_RATE = 0.001
# the scale of the entropy bonus
ENTROPY_BETA = 0.01
BATCH_SIZE = 8
# 각 transition의 할인된 총 보상을 추정하기 위해 벨만 방정식을 몇 스텝을 앞서 살펴봐야 하는지
REWARD_STEPS = 10


class PGN(nn.Module):
    '''
    앞선 02_cartpole_reinforce.py 에서의 PGN과 동일
    '''
    def __init__(self, input_size, n_actions):
        super(PGN, self).__init__()

        self.net = nn.Sequential(
            nn.Linear(input_size, 128),
            nn.ReLU(),
            nn.Linear(128, n_actions)
        )

    def forward(self, x):
        return self.net(x)


def smooth(old: Optional[float], val: float, alpha: float = 0.95) -> float:
    # 이 함수는 이전 스텝의 값을 95%, 새로운 값을 5%로 하여 반환
    # 왜 쓰는지 교재에 언급이 없음.
    if old is None:
        return val
    return old * alpha + (1-alpha)*val


if __name__ == "__main__":
    env = gym.make("CartPole-v0")
    writer = SummaryWriter(comment="-cartpole-pg")

    net = PGN(env.observation_space.shape[0], env.action_space.n)
    print(net)

    agent = ptan.agent.PolicyAgent(net, preprocessor=ptan.agent.float32_preprocessor,
                                   apply_softmax=True)
    # n-step ahead 할 때는 steps_count=n 주면 됨.
    exp_source = ptan.experience.ExperienceSourceFirstLast(
        env, agent, gamma=GAMMA, steps_count=REWARD_STEPS)

    optimizer = optim.Adam(net.parameters(), lr=LEARNING_RATE)

    total_rewards = []
    step_rewards = []
    step_idx = 0
    done_episodes = 0
    reward_sum = 0.0
    bs_smoothed = entropy = l_entropy = l_policy = l_total = None

    batch_states, batch_actions, batch_scales = [], [], []

    for step_idx, exp in enumerate(exp_source):
        reward_sum += exp.reward
        # baseline 을 평균으로 상정
        baseline = reward_sum / (step_idx + 1)
        writer.add_scalar("baseline", baseline, step_idx)
        batch_states.append(exp.state)
        batch_actions.append(int(exp.action))
        batch_scales.append(exp.reward - baseline)

        # handle new rewards
        new_rewards = exp_source.pop_total_rewards()
        if new_rewards:
            done_episodes += 1
            reward = new_rewards[0]
            total_rewards.append(reward)
            mean_rewards = float(np.mean(total_rewards[-100:]))
            print("%d: reward: %6.2f, mean_100: %6.2f, episodes: %d" % (
                step_idx, reward, mean_rewards, done_episodes))
            writer.add_scalar("reward", reward, step_idx)
            writer.add_scalar("reward_100", mean_rewards, step_idx)
            writer.add_scalar("episodes", done_episodes, step_idx)
            if mean_rewards > 195:
                print("Solved in %d steps and %d episodes!" % (step_idx, done_episodes))
                break

        if len(batch_states) < BATCH_SIZE:
            continue

        states_v = torch.FloatTensor(batch_states)
        batch_actions_t = torch.LongTensor(batch_actions)
        batch_scale_v = torch.FloatTensor(batch_scales)

        optimizer.zero_grad()
        logits_v = net(states_v)
        log_prob_v = F.log_softmax(logits_v, dim=1)
        log_prob_actions_v = batch_scale_v * log_prob_v[range(BATCH_SIZE), batch_actions_t]
        loss_policy_v = -log_prob_actions_v.mean()

        '''
        배치마다 엔트로피를 계산하여 loss 에서 엔트로피 값을 빼는 방식으로 entropy bonus 를 loss에 결합시킨다.
        엔트로피는 균일한 확률분포를 위한 최대값을 가지고 있고 우리는 이 최대값으로 학습을 하고 싶기 때문에 손실에서 빼야 한다.
        '''
        prob_v = F.softmax(logits_v, dim=1)
        entropy_v = -(prob_v * log_prob_v).sum(dim=1).mean()
        entropy_loss_v = -ENTROPY_BETA * entropy_v
        loss_v = loss_policy_v + entropy_loss_v

        loss_v.backward()
        optimizer.step()

        '''
        old policy 와 new policy 간 KL divergence 를 계산한다
        KL div는 하나의 확률 분포가 다른 기대 확률분포와 얼마나 다른지 측정하는 척도이다.
        이 예제에서는 최적화 단계 전후에 모델에 의해 반환된 정책을 비교하는 데 사용된다. 
        KL의 high spikes 는 대개 정책이 이전 정책과 너무 멀리 멀어졌음을 보여주는 나쁜 신호이다
        (NN은 고차원 공간에서 비선형 함수이므로 모델 가중치의 큰 변화는 정책에 매우 강력한 영향을 미칠 수 있음).
        '''
        # calc KL-div
        new_logits_v = net(states_v)
        new_prob_v = F.softmax(new_logits_v, dim=1)
        kl_div_v = -((new_prob_v / prob_v).log() * prob_v).sum(dim=1).mean()
        writer.add_scalar("kl", kl_div_v.item(), step_idx)

        '''
        학습 단계에서 gradient 에 대한 통계치 계산
        gradient 최대값, gradient에 L2 norm 적용한 값의 변화를 볼 수 있다.
        '''
        grad_max = 0.0
        grad_means = 0.0
        grad_count = 0
        for p in net.parameters():
            grad_max = max(grad_max, p.grad.abs().max().item())
            grad_means += (p.grad ** 2).mean().sqrt().item()
            grad_count += 1

        bs_smoothed = smooth(bs_smoothed, np.mean(batch_scales))
        entropy = smooth(entropy, entropy_v.item())
        l_entropy = smooth(l_entropy, entropy_loss_v.item())
        l_policy = smooth(l_policy, loss_policy_v.item())
        l_total = smooth(l_total, loss_v.item())

        writer.add_scalar("baseline", baseline, step_idx)
        writer.add_scalar("entropy", entropy, step_idx)
        writer.add_scalar("loss_entropy", l_entropy, step_idx)
        writer.add_scalar("loss_policy", l_policy, step_idx)
        writer.add_scalar("loss_total", l_total, step_idx)
        writer.add_scalar("grad_l2", grad_means / grad_count, step_idx)
        writer.add_scalar("grad_max", grad_max, step_idx)
        writer.add_scalar("batch_scales", bs_smoothed, step_idx)

        batch_states.clear()
        batch_actions.clear()
        batch_scales.clear()

    writer.close()

Results

보라색이 10-step ahead vanilla pg 의 보상 변화그래프이고, 하늘색이 REINFORCE 의 보상 변화그래프입니다. 엄청 다르진 않습니다.

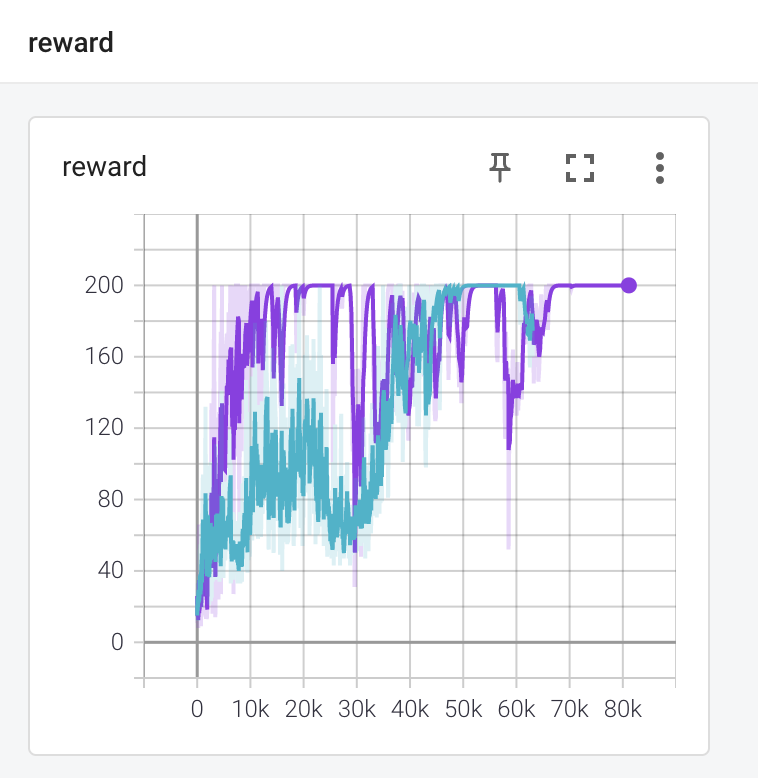
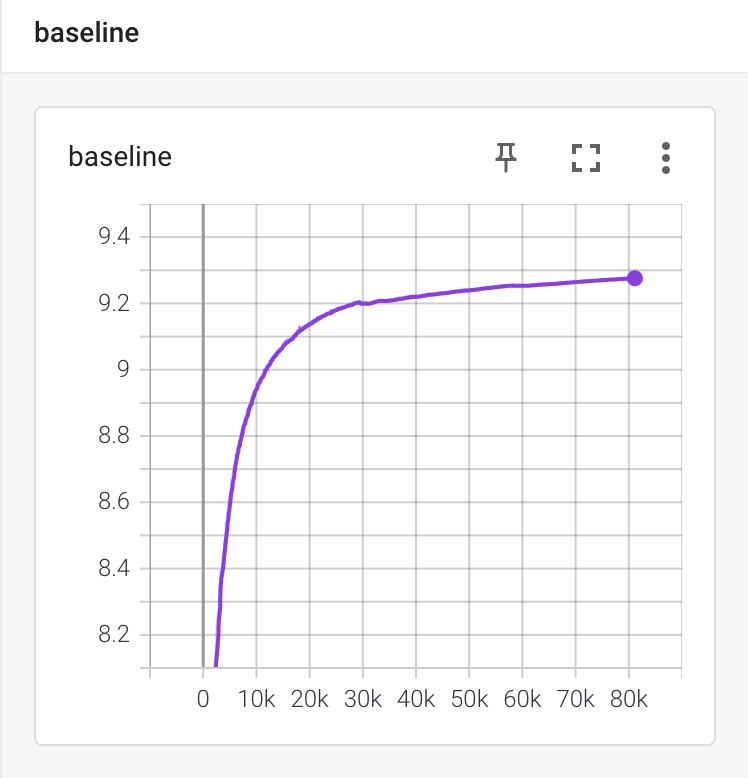
다음은 pg의 베이스라인으로 \(1 + 0.99 + 0.99^2 + ... + 0.99^9\) 로 수렴할 것입니다.

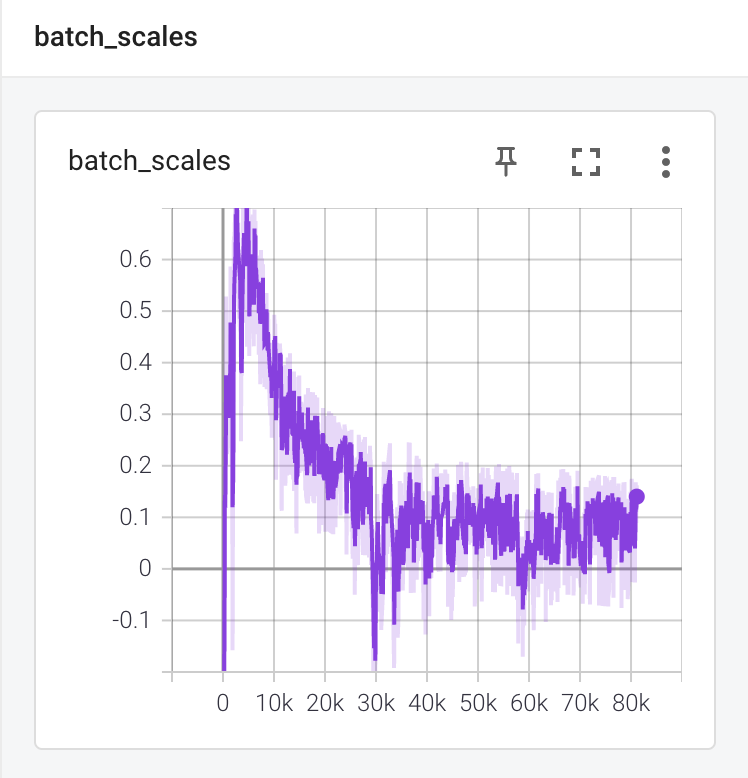
scale은 0 근처에서 요동치는 모습을 볼 수 있습니다.

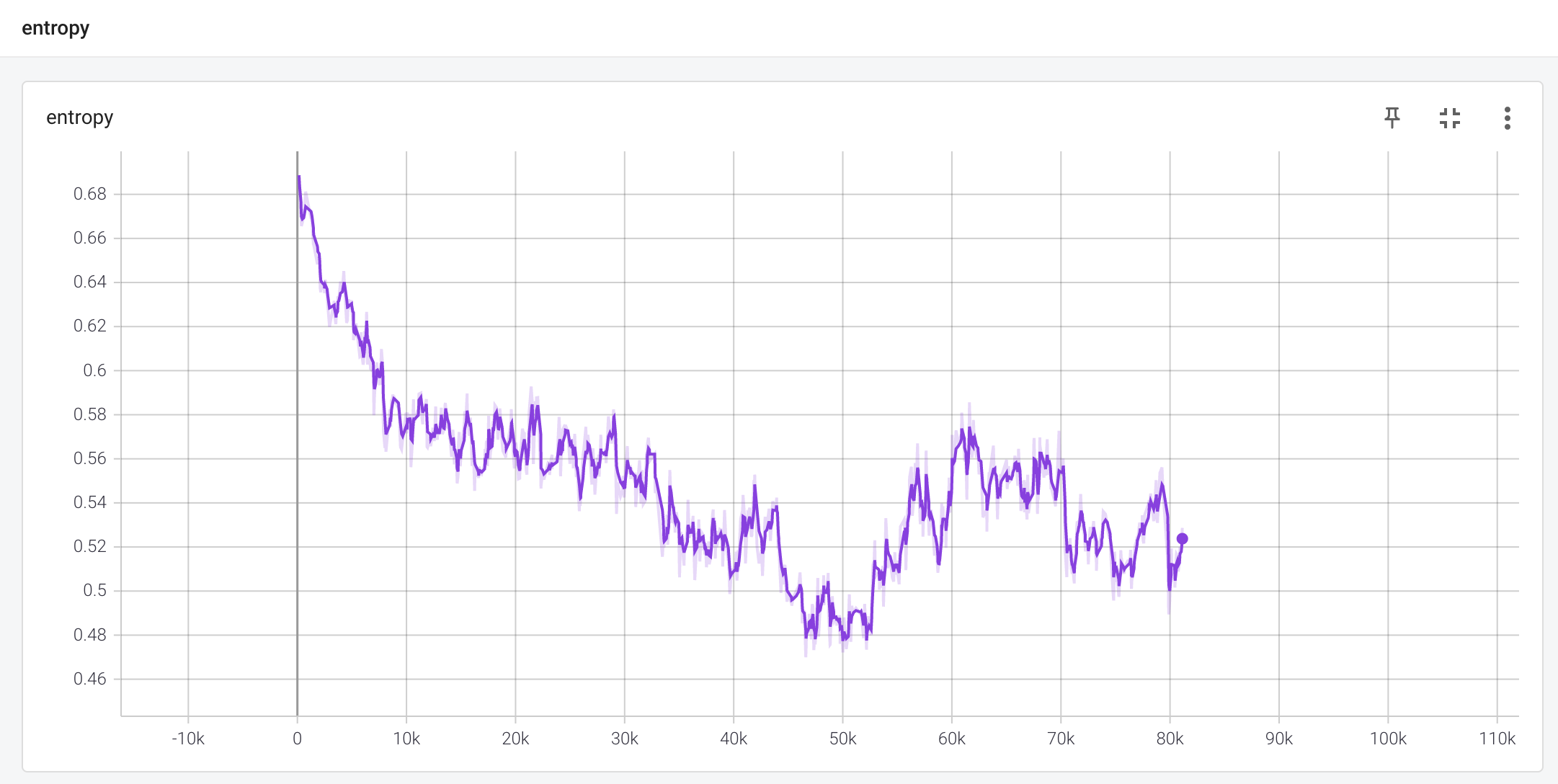
엔트로피는 0.69에서 0.52로 시간이 지남에 따라 떨어졌습니다. 시작 점은 두 행동의 최고 엔트로피로 약 0.69입니다.

\[H(\pi) = - \sum \pi(a|s) log \pi(a|s) = -(\frac{1}{2} \log (\frac{1}{2}) + \frac{1}{2} \log (\frac{1}{2})) \approx 0.69\]

학습 과정에서 엔트로피가 떨어진다는 것은 정책이 균일 분포에서 점점 더 결정론적인 행동으로 바뀌고 있다는 것을 보여줍니다.

다음은 policy loss, entropy loss, total loss 의 변화 그래프입니다.

entropy loss는 이전 엔트로피 차트를 상당히 반영하고 있습니다. 거울을 맞댄 형상입니다.

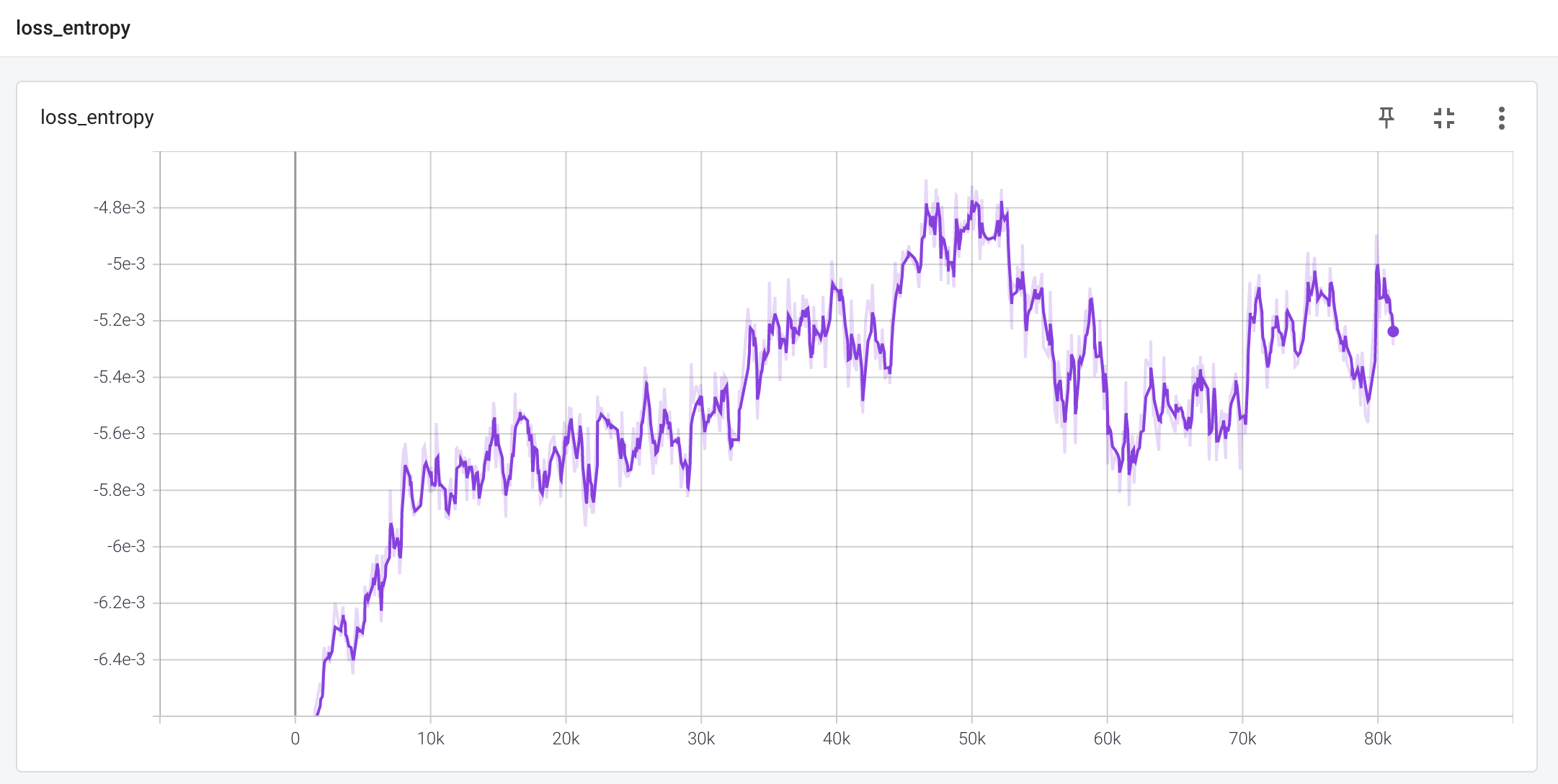
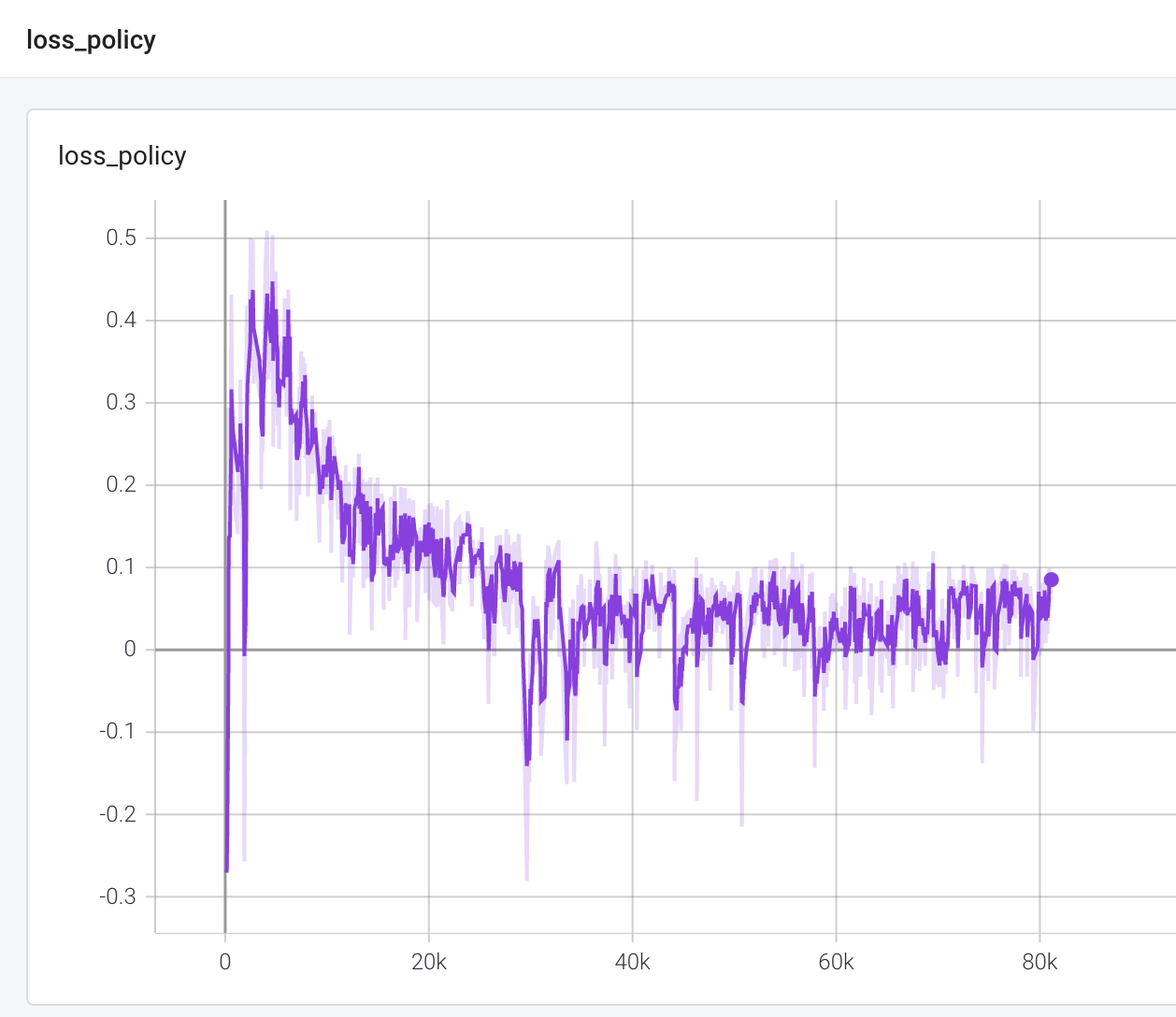
policy loss 는 배치 내에서 mean scale 과 policy gradient의 방향을 보여줍니다.

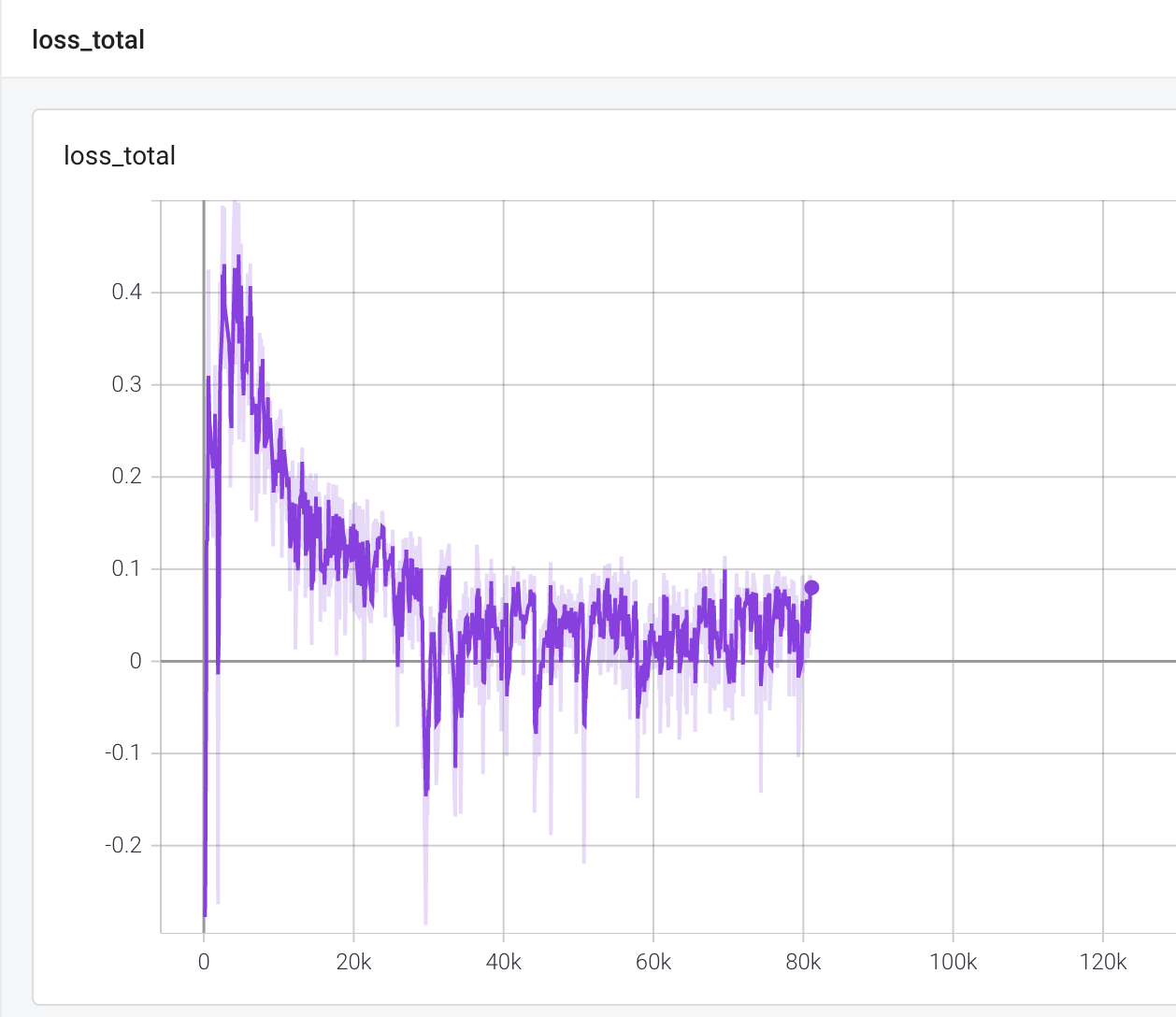
두 loss 를 더한 total loss는 다음과 같이 변화합니다.

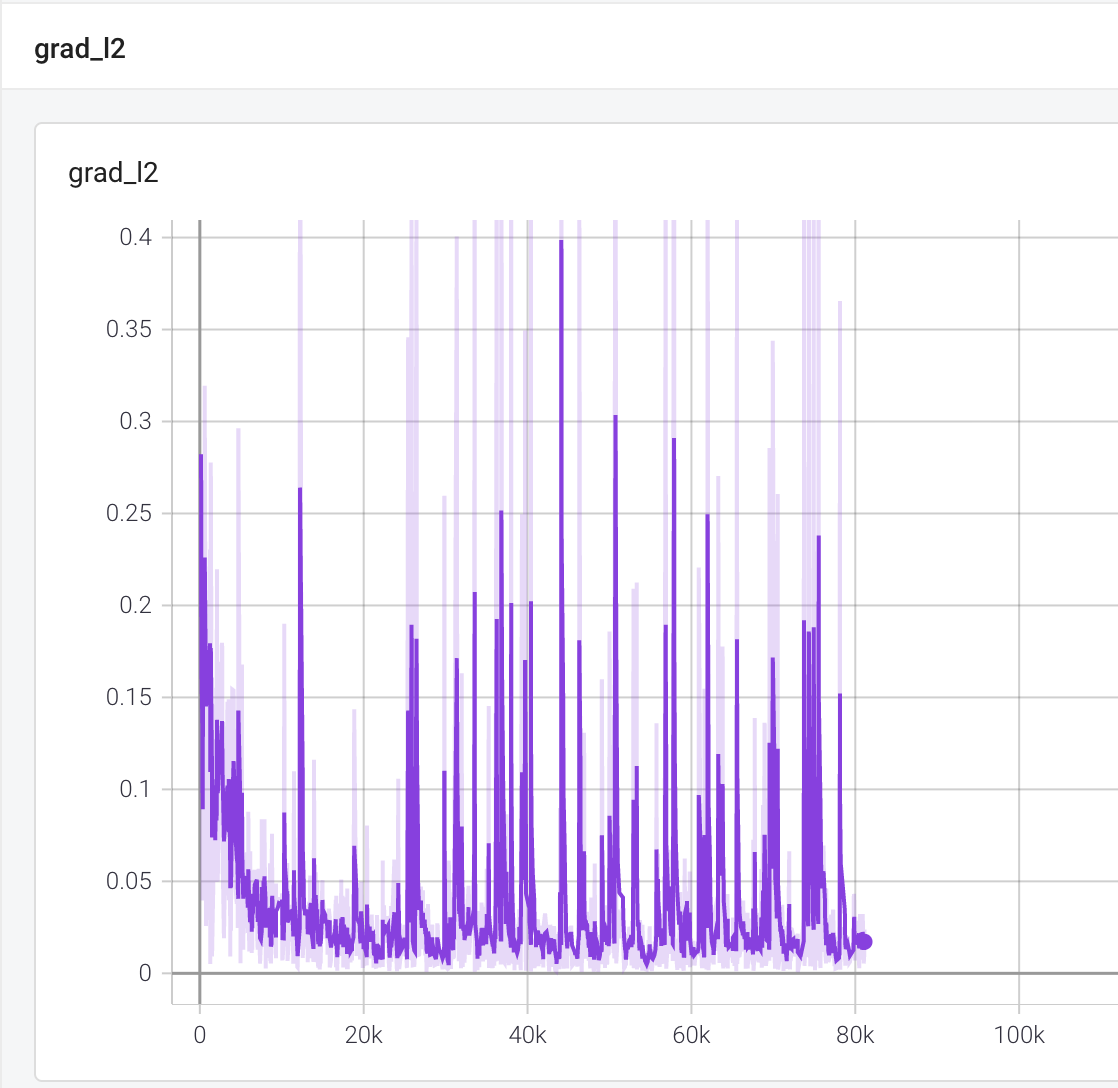
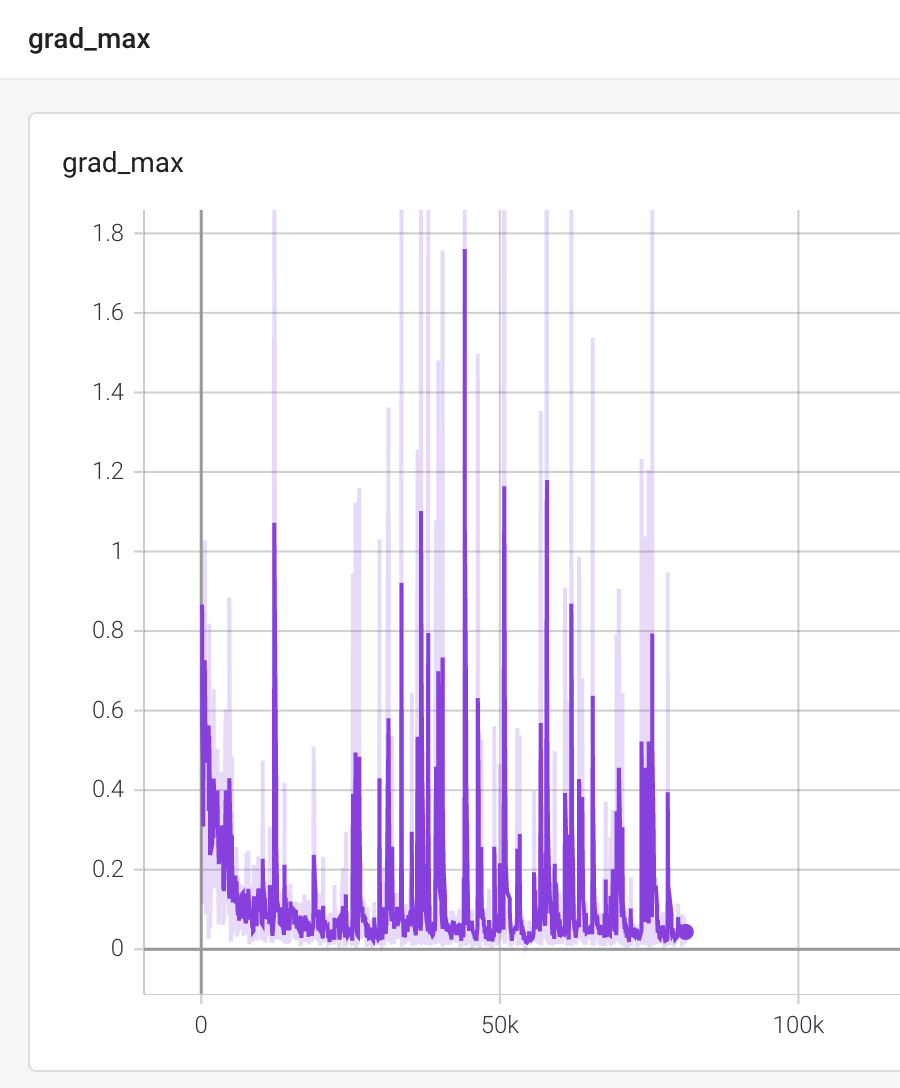
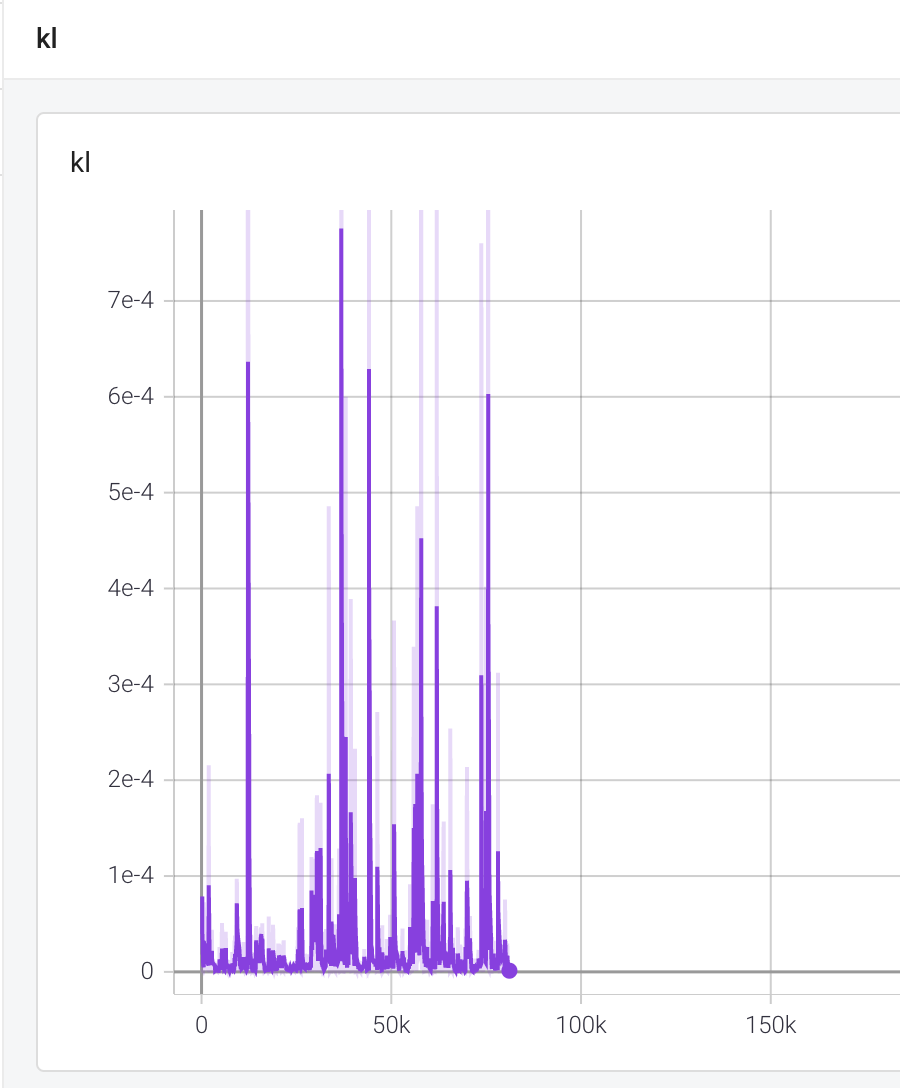
다음은 gradient 의 L2 값, 최대값, KL divergence 값입니다. 이 정도면 너무 크거나 너무 작지 않고 spike 도 적당한 것이라고 합니다. 세로축 단위를 보면 실제로 범위가 넓지 않음을 알 수 있습니다.

Policy gradient methods on Pong

Pong 에 하면 결과가 안 좋을 것이라는 것은 예상이 됩니다. DQN은 pong을 풀었는데 pg가 못한 것에 결과가 pg가 별로라는 말은 아닙니다. 다음 챕터에서 나올 actor-critic model은 성능이 좋습니다. 또한, 성공치 못한 결과도 가치가 있습니다. 좋지 않은 수렴 변화 그래프를 볼 수 있습니다.

Implemenation

Chapter11/05_pong_pg.py 에 구현 코드가 있습니다. 이전 코드와 다른 세 가지는 다음과 같습니다.

baseline 을 모든 예제가 아니라 1M 과거 transitions 에 대한 이동 평균으로 함
동시에 여러 환경 사용
학습 안정성을 향상시키기 위해 gradient clipping 함

#!/usr/bin/env python3
import gym
import ptan
import numpy as np
import argparse
import collections
from tensorboardX import SummaryWriter

import torch
import torch.nn.functional as F
import torch.nn.utils as nn_utils
import torch.optim as optim

from lib import common

GAMMA = 0.99
LEARNING_RATE = 0.0001
ENTROPY_BETA = 0.01
BATCH_SIZE = 128

REWARD_STEPS = 10
BASELINE_STEPS = 1000000
GRAD_L2_CLIP = 0.1

ENV_COUNT = 32


def make_env():
    return ptan.common.wrappers.wrap_dqn(gym.make("PongNoFrameskip-v4"))


class MeanBuffer:
    '''이동평균 계산을 빨리하기 위해서 deque buffer를 사용
    '''
    def __init__(self, capacity):
        self.capacity = capacity
        self.deque = collections.deque(maxlen=capacity)
        self.sum = 0.0

    def add(self, val):
        if len(self.deque) == self.capacity:
            self.sum -= self.deque[0]
        self.deque.append(val)
        self.sum += val

    def mean(self):
        if not self.deque:
            return 0.0
        return self.sum / len(self.deque)


if __name__ == "__main__":
    parser = argparse.ArgumentParser()
    parser.add_argument("--cuda", default=False, action="store_true", help="Enable cuda")
    parser.add_argument("-n", '--name', required=True, help="Name of the run")
    args = parser.parse_args()
    device = torch.device("cuda" if args.cuda else "cpu")

    # 여러 개의 환경 사용하기 위한 작업
    envs = [make_env() for _ in range(ENV_COUNT)]
    writer = SummaryWriter(comment="-pong-pg-" + args.name)

    net = common.AtariPGN(envs[0].observation_space.shape, envs[0].action_space.n).to(device)
    print(net)

    agent = ptan.agent.PolicyAgent(net, apply_softmax=True, device=device)
    # 여러 개의 환경을 넣어도 자동으로 transition을 받을 수 있다.
    exp_source = ptan.experience.ExperienceSourceFirstLast(envs, agent, gamma=GAMMA, steps_count=REWARD_STEPS)

    optimizer = optim.Adam(net.parameters(), lr=LEARNING_RATE, eps=1e-3)

    total_rewards = []
    step_idx = 0
    done_episodes = 0
    train_step_idx = 0
    baseline_buf = MeanBuffer(BASELINE_STEPS)

    batch_states, batch_actions, batch_scales = [], [], []
    m_baseline, m_batch_scales, m_loss_entropy, m_loss_policy, m_loss_total = [], [], [], [], []
    m_grad_max, m_grad_mean = [], []
    sum_reward = 0.0

    # RewardTracker 는 mean reward 계산하고 report, 추가로 mean_reward > stop_reward 일 때 종료시킴
    with common.RewardTracker(writer, stop_reward=18) as tracker:
        for step_idx, exp in enumerate(exp_source):
            baseline_buf.add(exp.reward)
            baseline = baseline_buf.mean()
            batch_states.append(np.array(exp.state, copy=False))
            batch_actions.append(int(exp.action))
            batch_scales.append(exp.reward - baseline)

            # handle new rewards
            new_rewards = exp_source.pop_total_rewards()
            if new_rewards:
                if tracker.reward(new_rewards[0], step_idx):
                    break

            if len(batch_states) < BATCH_SIZE:
                continue

            train_step_idx += 1
            states_v = torch.FloatTensor(np.array(batch_states, copy=False)).to(device)
            batch_actions_t = torch.LongTensor(batch_actions).to(device)

            scale_std = np.std(batch_scales)
            batch_scale_v = torch.FloatTensor(batch_scales).to(device)

            optimizer.zero_grad()
            logits_v = net(states_v)
            log_prob_v = F.log_softmax(logits_v, dim=1)
            log_prob_actions_v = batch_scale_v * log_prob_v[range(BATCH_SIZE), batch_actions_t]
            loss_policy_v = -log_prob_actions_v.mean()

            prob_v = F.softmax(logits_v, dim=1)
            entropy_v = -(prob_v * log_prob_v).sum(dim=1).mean()
            entropy_loss_v = -ENTROPY_BETA * entropy_v
            loss_v = loss_policy_v + entropy_loss_v
            loss_v.backward()
            # gradient clipping for training stability
            nn_utils.clip_grad_norm_(net.parameters(), GRAD_L2_CLIP)
            optimizer.step()

            # calc KL-div
            new_logits_v = net(states_v)
            new_prob_v = F.softmax(new_logits_v, dim=1)
            kl_div_v = -((new_prob_v / prob_v).log() * prob_v).sum(dim=1).mean()
            writer.add_scalar("kl", kl_div_v.item(), step_idx)

            grad_max = 0.0
            grad_means = 0.0
            grad_count = 0
            for p in net.parameters():
                grad_max = max(grad_max, p.grad.abs().max().item())
                grad_means += (p.grad ** 2).mean().sqrt().item()
                grad_count += 1

            writer.add_scalar("baseline", baseline, step_idx)
            writer.add_scalar("entropy", entropy_v.item(), step_idx)
            writer.add_scalar("batch_scales", np.mean(batch_scales), step_idx)
            writer.add_scalar("batch_scales_std", scale_std, step_idx)
            writer.add_scalar("loss_entropy", entropy_loss_v.item(), step_idx)
            writer.add_scalar("loss_policy", loss_policy_v.item(), step_idx)
            writer.add_scalar("loss_total", loss_v.item(), step_idx)
            writer.add_scalar("grad_l2", grad_means / grad_count, step_idx)
            writer.add_scalar("grad_max", grad_max, step_idx)

            batch_states.clear()
            batch_actions.clear()
            batch_scales.clear()

    writer.close()

Results

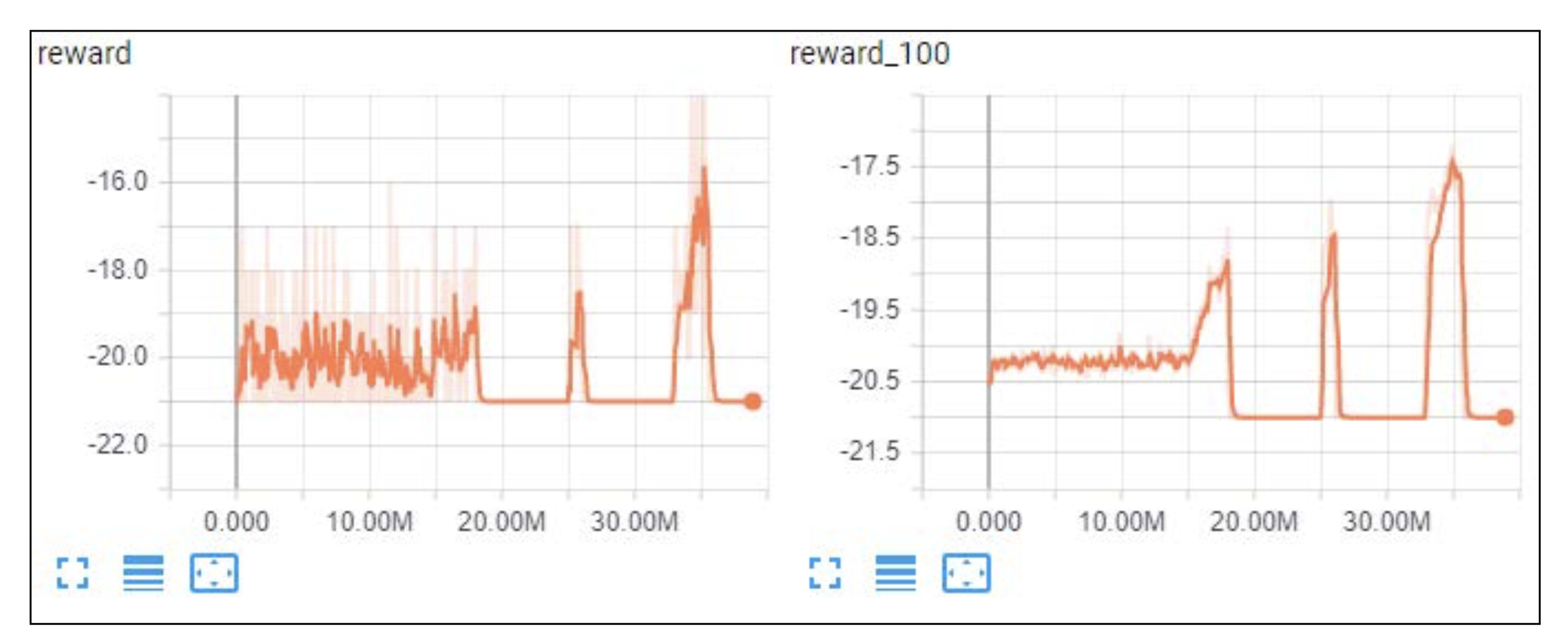
예상했던 바와 같이 보상 점수는 좋지 않습니다. -21 보다는 안 내려가는 동일한 모습을 보여주고 있습니다.

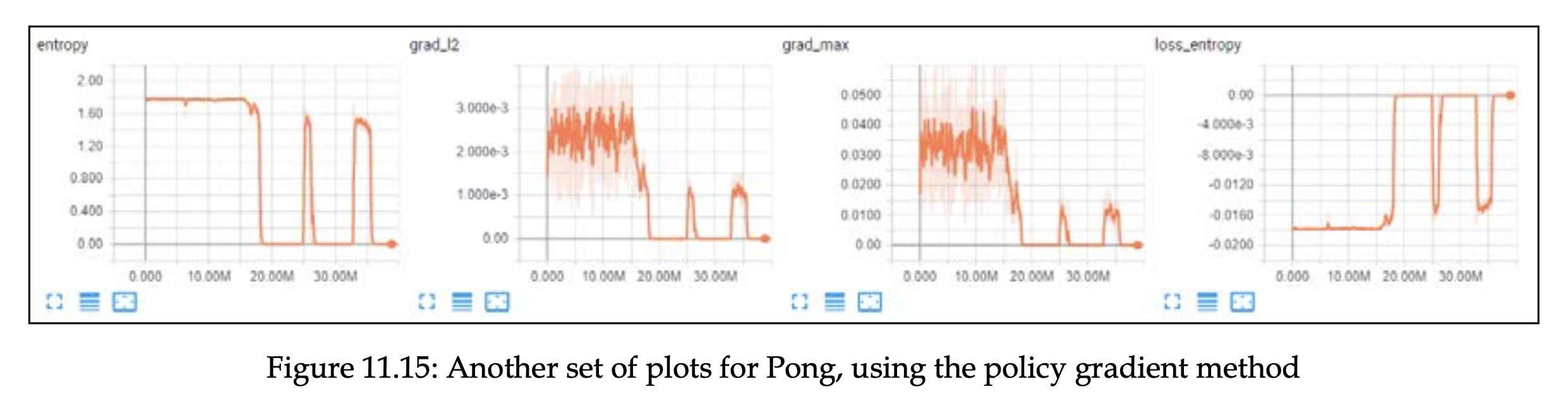
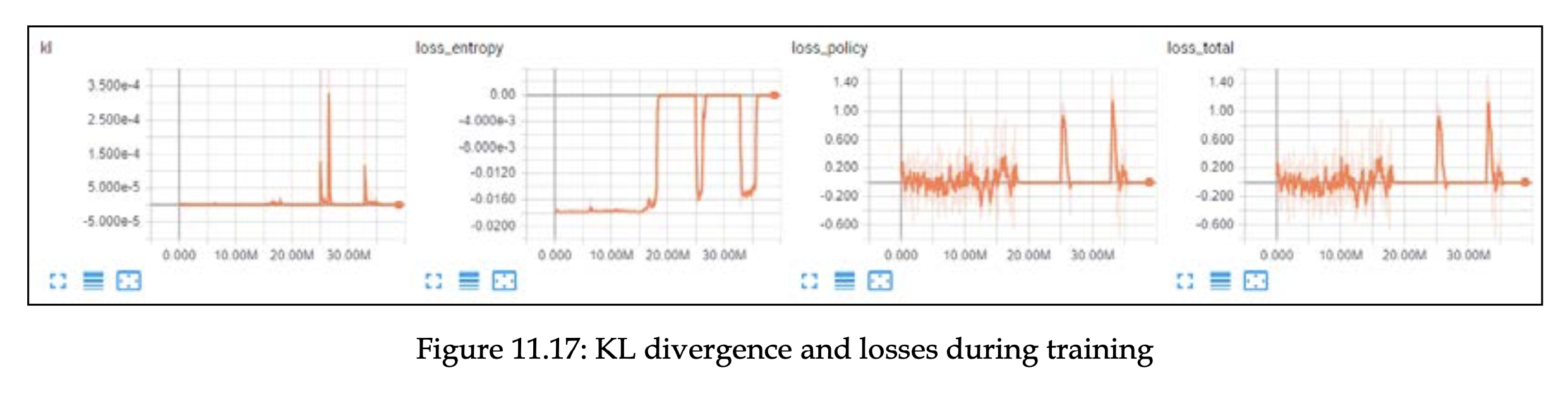
엔트로피 관련 플랏들입니다. 엔트로피가 0 일 때, 나머지 플랏에서도 점수가 0인 것을 확인할 수 있습니다. 이는 에이전트가 행동에 대해 100% 확신이 있다는 의미입니다. 이 기간에 gradient 도 0이었는데, 이러한 평탄한 지역에서 학습 과정을 회복할 수 있었다는 사실이 주목할만 합니다.

다음 차트에서는 베이스라인이 보상을 대부분 따르고 동일한 패턴을 보여준다는 것을 확인할 수 있습니다.

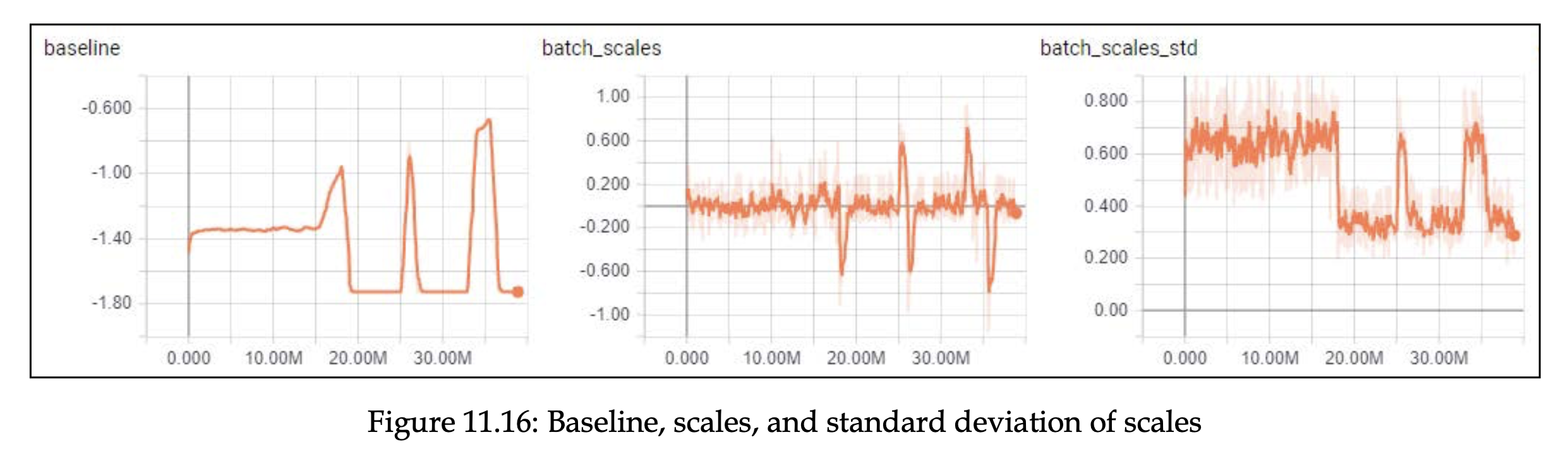
KL 플랏에서는 zero entropy 전환 시점 사이에 큰 spike 를 가지는데 이는 정책이 분포를 반환하는 과정에서 심한 점프로 인해 어려움을 겪었음을 보여줍니다.

Summary

이 챕터에서는 RL 문제를 푸는 다른 방법인 Policy Gradient 에 대해 알아보았습니다.

pg의 기본 방법인 REINFORCE 에 대해 다룸 -> CartPole 에서 실험
vanilla pg 모델로 CartPole, Pong 에서 실험
- CartPole 은 잘하지만, Pong 에서는 잘 못함

다음 챕터에서는 policy-based 방법에 value-based 방법을 결합하여 policy gradient 의 안정성을 향상시킨 actor-critic 방법에 대해 다룰 예정입니다.

References

Deep Reinforcement Learning Hands On 2/E Chapter 11 : Policy Gradients - an Alternative

ptan ExperienceSource code